Câu hỏi
Đường cong hình bên là đồ thị một trong 4 hàm số được liệt kê ở 4 phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
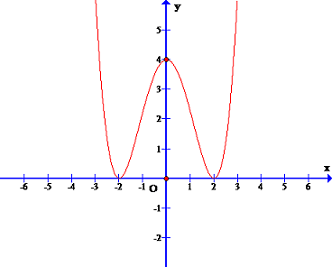
- A \(y = \dfrac{1}{4}{x^4} - 2{x^2} + 4\)
- B \(y = - \dfrac{1}{4}{x^4} + 2{x^2} + 4\)
- C \(y = {x^3} - 3x - 2\)
- D \(y = {x^2} - 2x - 3\)
Lời giải chi tiết:
- Nhận dạng đồ thị hàm số (đa thức bậc ba, bậc bốn, phân thức …)
- Nhận xét dấu của hệ số bậc cao nhất: Nếu \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \) thì \(a > 0\), nếu \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \) thfi \(a < 0\). Hình dạng đồ thị là của hàm trùng phương bậc 4 nên loại đáp án C và D.
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \) nên \(a > 0\), do đó loại đáp án B.
Vậy đáp án đúng là A.
Chọn A.
Câu hỏi trước
