Câu hỏi
Cho bốn điểm A(1;1), B(2;-1), C(4;3), D(3;5). Hãy chọn mệnh đề đúng:
- A Tứ giác ABCD là hình bình hành.
- B Điểm
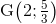 là trọng tâm của tam giác BCD.
là trọng tâm của tam giác BCD. - C
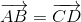
- D
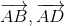 cùng phương.
cùng phương.
Lời giải chi tiết:
Ta có:
$$\eqalign{ & \overrightarrow {AB} = \left( {1; - 2} \right) \Rightarrow AB = \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \cr & \overrightarrow {DC} = \left( {1; - 2} \right) \Rightarrow CD = \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \cr} $$
Vậy 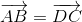 nên tứ giác ABCD là hình bình hành. Đáp án A đúng.
nên tứ giác ABCD là hình bình hành. Đáp án A đúng.
Đáp án B sai vì: Trọng tâm của tam giác BCD là:
$$ \left\{\begin{matrix}{x_G} = {{{x_B} + x{ _C} + {x_D}} \over 3}\\ {y_G} = {{{y_B} + {y_C} + {y_D}} \over 3}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}{x_G} = {{2 + 4 + 3} \over 3} = 3 \\ {y_G} = {{ - 1 + 3 + 5} \over 3} = {7 \over 3}\end{matrix}\right.v$$
Đáp án C sai vì: 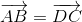
Đáp án D sai vì ABCD là hình bình hành, dựa vào hình vẽ ta thấy luôn
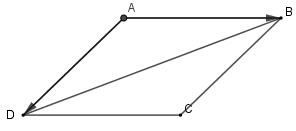
Chọn A







