Phương pháp giải:

Độ lớn gia tốc của vật dao động: \(a = {\omega ^2}x = \dfrac{g}{{\Delta {\rm{l}}}}x\)

Sử dụng vòng tròn lượng giác và công thức: \(\Delta t = \dfrac{{\Delta \varphi .T}}{{2\pi }}\)

Lời giải chi tiết:

Độ lớn gia tốc của vật là: \(a = \left| {\dfrac{g}{{\Delta {\rm{l}}}}x} \right| = \dfrac{g}{{0,5A}}\left| x \right| = \dfrac{{2g\left| x \right|}}{A}\)Độ lớn gia tốc của vật đó lớn hơn hoặc bằng gia tốc trọng trường g, ta có:

\(a \ge g \Rightarrow \dfrac{{2g\left| x \right|}}{A} \ge g \Rightarrow \left| x \right| \ge \dfrac{A}{2} \Rightarrow \left\{ \begin{array}{l}x \ge \dfrac{A}{2}\\x \le  - \dfrac{A}{2}\end{array} \right.\)

Ta có vòng tròn lượng giác:

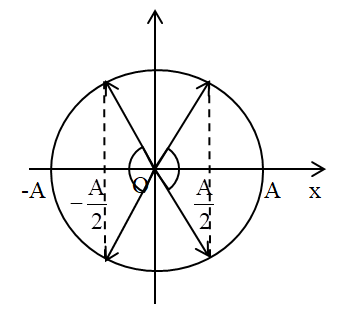
Từ vòng tròn lượng giác, ta thấy trong 1 chu kì, vật có độ lớn gia tốc lớn hơn hoặc bằng gia tốc trọng trường khi vecto quay được góc: \(\Delta \varphi  = 2.\dfrac{{2\pi }}{3} = \dfrac{{4\pi }}{3}\,\,\left( {rad} \right)\)

Thời gian vật có độ lớn gia tốc lớn hơn hoặc bằng gia tốc trọng trường trong 1 chu kì là:

\(\Delta t = \dfrac{{\Delta \varphi .T}}{{2\pi }} = \dfrac{{\dfrac{{4\pi }}{3}.T}}{{2\pi }} = \dfrac{{2T}}{3}\)

Chọn D.