Phương pháp giải:

Xét phương trình hoành độ giao điểm \(\left( * \right)\)  của hai đồ thị hàm số.

Hai đồ thị hàm số cắt nhau tại một điểm duy nhất có hoành độ dương \( \Leftrightarrow \left( * \right)\) có nghiệm dương duy nhất.

Lời giải chi tiết:

Phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho là:

\(\begin{array}{l}{x^3} + \left( {m + 2} \right)x + 1 = 2x - 1 \Leftrightarrow {x^3} + mx + 2 = 0\,\,\,\,\\ \Leftrightarrow mx =  - {x^3} - 2\\ \Leftrightarrow m =  - {x^2} - \frac{2}{x}\,\,\,\,\,\,\,\,\,\,\,\left( {x \ne 0} \right)\,\,\,\,\left( * \right)\end{array}\)

Hai đồ thị của hai hàm số đã cho cắt nhau tại một điểm duy nhất có hoành độ dương \( \Leftrightarrow \left( * \right)\) có một nghiệm  duy nhất và nghiệm đó là nghiệm dương.

Số nghiệm  của phương trình \(\left( * \right)\) là số giao điểm của đường thẳng \(y = m\) và đồ thị hàm số \(y =  - {x^2} - \frac{2}{x}\) trên \(\left( { - \infty ;\,\,0} \right) \cup \left( {0; + \infty } \right).\)

Xét hàm số \(y =  - {x^2} - \frac{2}{x}\) trên \(\left( { - \infty ;\,\,0} \right) \cup \left( {0; + \infty } \right)\) ta có:

\(y' =  - 2x + \frac{2}{{{x^2}}} \Rightarrow y' = 0 \Leftrightarrow  - 2{x^3} + 2 = 0 \Leftrightarrow x = 1.\)

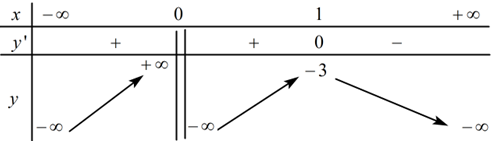
Ta có BBT:

Dựa vào bảng biến thiên ta có không có giá trị m thỏa mãn bài toán.

Chọn D.