Câu hỏi
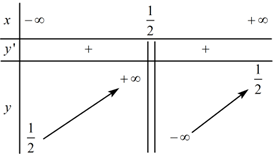
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên
Hàm số \(y = f\left( x \right)\) là hàm nào dưới đây?
- A \(y = \frac{{x + 2}}{{2x - 1}}.\)
- B \(y = \frac{{x - 2}}{{2x - 1}}.\)
- C \(y = \frac{{ - x + 2}}{{2x - 1}}.\)
- D \(y = \frac{{ - x - 2}}{{2x - 1}}.\)
Phương pháp giải:
Dựa vào bảng biến thiên để tìm các đường tiệm cận của đồ thị hàm số và tính đơn điệu của hàm số, từ đó suy ra công thức của hàm số \(y = f\left( x \right)\).
Lời giải chi tiết:
Dựa vào BBT ta có \(\mathop {\lim }\limits_{x \to \frac{1}{2}} f\left( x \right) = \infty \Rightarrow x = \frac{1}{2}\) là tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to \infty } f\left( x \right) = \frac{1}{2} \Rightarrow y = \frac{1}{2}\) là tiệm cận ngang của đồ thị hàm số.
\( \Rightarrow \) loại đáp án C và D.
Lại thấy hàm số đồng biến trên \(\left( { - \infty ;\,\,\frac{1}{2}} \right)\) và \(\left( {\frac{1}{2}; + \infty } \right)\)
+) Xét đáp án A: \(y = \frac{{x + 2}}{{2x - 1}}\) ta có:\(y' = \frac{{ - 1 - 2.2}}{{{{\left( {2x - 1} \right)}^2}}} = - \frac{5}{{{{\left( {2x - 1} \right)}^2}}} < 0 \Rightarrow \) loại đáp án A.
\( \Rightarrow y = \frac{{x - 2}}{{2x - 1}}\) là hàm số cần tìm.
Chọn B.