Câu hỏi
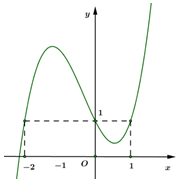
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)\) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng ?
- A \(a > 0;\,\,b > 0;\,\,c < 0;\,\,d > 0.\)
- B \(a < 0;\,\,b < 0;\,\,c < 0;\,\,d > 0.\)
- C \(a > 0;\,\,b < 0;\,\,c < 0;\,\,d > 0.\)
- D \(a > 0;\,\,b < 0;\,\,c > 0;\,\,d > 0.\)
Phương pháp giải:
Dựa vào đồ thị nhận biết nét cuối của đồ thị hàm số và các điểm mà đồ thị hàm số đi qua để xác định dấu của các hệ số.
Lời giải chi tiết:
Đồ thị hàm số \(y = a{x^3} + b{x^2} + cx + d\) có nét cuối đi lên \( \Rightarrow a > 0 \Rightarrow \) loại đáp án B.
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương \( \Rightarrow d > 0.\)
Ta có: \(y' = 3a{x^2} + 2bx + c \Rightarrow y' = 0 \Leftrightarrow 3a{x^2} + 2bx + c = 0\,\,\,\left( * \right)\)
Đồ thị hàm số \(y = a{x^3} + b{x^2} + cx + d\) có 2 điểm cực trị trái dấu và điểm cực trị có hoành độ âm cách xa điểm \(O\) hơn điểm cực trị có hoành độ dương
\( \Rightarrow \left\{ \begin{array}{l} - \frac{b}{a} < 0\\ac < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{b}{a} > 0\\ac < 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b > 0\\c < 0\end{array} \right.\)
Chọn A.