Phương pháp giải:

- Dựa vào từng giả thiết tìm tập hợp các điểm biểu diễn số phức \(z\).

- Gọi \(M,\,\,A\) lần lượt là các điểm biểu diễn số phức \(z\) và \(2\), khi đó ta có \(\left| {z - 2} \right| = MA\).

- Vẽ hình và tìm vị trí của \(M\) để \(MA\) lớn nhất.

Lời giải chi tiết:

Đặt \(z = a + bi\)\( \Rightarrow \overline z  = a - bi.\)

Theo bài ra ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,\left( {z - 3 - 3i} \right)\left( {\overline z  - 3 + 3i} \right) = 1\\ \Leftrightarrow \left[ {a - 3 + \left( {b - 3} \right)i} \right]\left[ {a - 3 - \left( {b - 3} \right)i} \right] = 1\\ \Leftrightarrow {\left( {a - 3} \right)^2} - \left( {a - 3} \right)\left( {b - 3} \right)i + \left( {a - 3} \right)\left( {b - 3} \right)i + {\left( {b - 3} \right)^2} = 1\\ \Rightarrow {\left( {a - 3} \right)^2} + {\left( {b - 3} \right)^2} = 1\end{array}\)

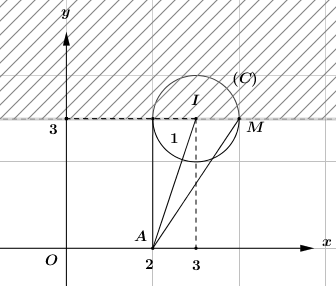
\( \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(z\) là đường tròn \(\left( C \right)\) tâm \(I\left( {3;3} \right)\), bán kính \(R = 1\).

Lại theo giả thiết ta có:

\(\begin{array}{l}\,\,\,\,\,\,\left| {\overline z  + 2i} \right| \le \left| {z - 4i} \right|\\ \Leftrightarrow \left| {a - \left( {b - 2} \right)i} \right| \le \left| {a + \left( {b - 4} \right)i} \right|\\ \Leftrightarrow \sqrt {{a^2} + {{\left( {b - 2} \right)}^2}}  \le \sqrt {{a^2} + {{\left( {b - 4} \right)}^2}} \\ \Leftrightarrow {a^2} + {\left( {b - 2} \right)^2} \le {a^2} + {\left( {b - 4} \right)^2}\\ \Leftrightarrow {a^2} + {b^2} - 4b + 4 \le {a^2} + {b^2} - 8b + 16\\ \Leftrightarrow 4b \le 12\\ \Leftrightarrow b \le 3\end{array}\)

\( \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(z\) là đường tròn nửa mặt phẳng bờ là đường thẳng \(y = 3\) chứa trục \(Ox\) (Tính cả bờ).

Gọi \(M,\,\,A\) lần lượt là các điểm biểu diễn số phức \(z\) và \(2\), khi đó ta có \(\left| {z - 2} \right| = MA\).

Dựa vào hình vẽ ta thấy \(M{A_{\max }} \Leftrightarrow M\left( {4;3} \right)\). Khi đó \(MA = \sqrt {{2^2} + {3^2}}  = \sqrt {13} \).

Chọn A.