Phương pháp giải:

- Tính diện tích của \(\left( H \right)\).

- Gọi \(B\left( {{x_0};0} \right) \in d \cap Ox\), tính diện tích \({S_{OAB}}\).

- Dựa vào giả thiết suy ra \({S_{OAB}} = \dfrac{1}{2}{S_{\left( H \right)}}\), tìm \({x_0}\), sau đó tìm \(a;\,\,b\).

Lời giải chi tiết:

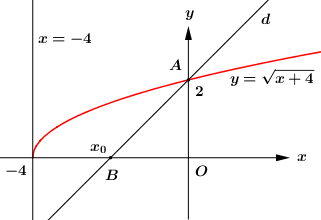
Xét phương trình hoành độ giao điểm của đồ thị hàm số \(y = \sqrt {x + 4} \) và trục hoành:

\(\sqrt {x + 4}  = 0 \Leftrightarrow x =  - 4\).

Suy ra \({S_{\left( H \right)}} = \int\limits_{ - 4}^0 {\left| {\sqrt {x + 4}  - 0} \right|dx}  = \int\limits_{ - 4}^0 {\sqrt {x + 4} dx}  = \dfrac{{16}}{3}\).

Ta có: \(A\left( {0;2} \right)\) chính là giao điểm của đường thẳng \(d\) và đồ thị hàm số \(y = \sqrt {x + 4} \).

Gọi \(B\left( {{x_0};0} \right) \in d \cap Ox\), ta có \({S_{OAB}} = \dfrac{1}{2}.OA.OB = \dfrac{1}{2}.2.\left| {{x_0}} \right| = \left| {{x_0}} \right|\).

Để đường thẳng \(d:\,\,ax + by - 16 = 0\) và chia \(\left( H \right)\) thành hai phần có diện tích bằng nhau thì \({x_0} < 0\) và \({S_{OAB}} = \dfrac{1}{2}{S_{\left( H \right)}}\).

\( \Rightarrow \left| {{x_0}} \right| = \dfrac{8}{3} \Leftrightarrow {x_0} =  - \dfrac{8}{3}\) (Do \({x_0} < 0\)).

Suy ra đường thẳng \(d\) đi qua \(A\left( {0;2} \right)\) và \(B\left( { - \dfrac{8}{3};0} \right)\), ta có: \(\left\{ \begin{array}{l}2b - 16 = 0\\ - \dfrac{8}{3}a - 16 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 8\\a =  - 6\end{array} \right.\).

Vậy \(a + 2b =  - 6 + 2.8 = 10\).

Chọn A.