Câu hỏi
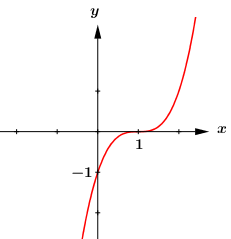
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(\left( C \right)\) như hình vẽ. Hỏi \(\left( C \right)\) là đồ thị của hàm số nào?
- A \(y = {x^3} - 1\)
- B \(y = {x^3} + 1\)
- C \(y = {\left( {x - 1} \right)^3}\)
- D \(y = {\left( {x + 1} \right)^3}\)
Phương pháp giải:
Dựa vào điểm đi qua và điểm uốn của đồ thị hàm số.
Lời giải chi tiết:
Đồ thị hàm số đi qua điểm \(\left( {0; - 1} \right)\) nên loại đáp án B và D.
Đồ thị hàm số có điểm uốn \(\left( {1;0} \right)\).
Xét đáp án A ta có \(y' = 3{x^2} \Rightarrow y'' = 6x = 0\) \( \Leftrightarrow x = 0 \Rightarrow y = 0\)\( \Rightarrow \) Điểm uốn của đồ thị hàm số là \(\left( {0;0} \right)\).
Xét đáp án C ta có \(y' = 3{\left( {x - 1} \right)^2} \Rightarrow y'' = 6\left( {x - 1} \right) = 0\) \( \Leftrightarrow x = 1 \Rightarrow y = 0\)\( \Rightarrow \) Điểm uốn của đồ thị hàm số là \(\left( {1;0} \right)\).
Vậy đồ thị \(\left( C \right)\) như trên là đồ thị của hàm số \(y = {\left( {x - 1} \right)^3}\).
Chọn C.







