Câu hỏi
Cho đồ thị hàm số \(y = \sin x\) như hình dưới, tìm tất cả các số thực \(x \in \left[ { - \dfrac{\pi }{2};\,\,2\pi } \right]\) để \(\sin \left| x \right| > 0.\)
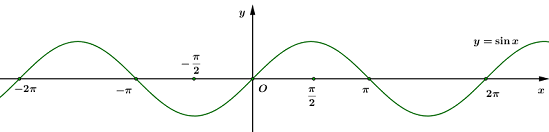
- A \(\left( {0;\,\,\pi } \right)\)
- B \(\left( { - \dfrac{\pi }{2};\,\,\dfrac{\pi }{2}} \right)\)
- C \(\left[ { - \dfrac{\pi }{2};\,\,0} \right) \cup \left( {0;\,\,\pi } \right)\)
- D \(\left( { - \dfrac{\pi }{2};\,\,0} \right) \cup \left( {0;\,\,\pi } \right)\)
Phương pháp giải:
Từ đồ thị hàm số đã cho, suy ra đồ thị hàm số \(y = \sin \left| x \right|\) bằng cách giữ lại phần đồ thị phía bên phải trục tung và lấy đối xứng phần đồ thị đó qua trục tung.
Lời giải chi tiết:
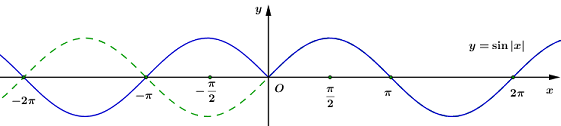
Dựa vào đồ thị hàm số \(y = \sin \left| x \right|\) ta thấy \(\sin \left| x \right| > 0 \Leftrightarrow \left[ \begin{array}{l} - \dfrac{\pi }{2} < x < 0\\0 < x < \pi \end{array} \right..\)
Chọn D.
Câu hỏi trước
