Phương pháp giải:

- Lập BBT của hàm số \(y = 2{x^2} - 3x + 4m + 5\) trên \(\left[ { - 1;2} \right]\).

- Chia các TH, xác định GTLN của hàm số \(y = \left| {2{x^2} - 3x + 4m + 5} \right|\), từ đó xác định \(a,\,b\) và kết luận.

Lời giải chi tiết:

Xét hàm số \(y = 2{x^2} - 3x + 4m + 5\) ta có: \(f'\left( x \right) = 4x - 3 = 0 \Leftrightarrow x = \dfrac{3}{4} \in \left[ { - 1;2} \right]\)

BBT:

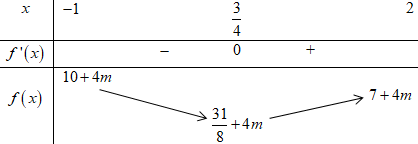
TH1: \(\dfrac{{31}}{8} + 4m \ge 0 \Leftrightarrow m \ge  - \dfrac{{31}}{{32}}\).

Khi đó hàm số \(y = \left| {2{x^2} - 3x + 4m + 5} \right|\) đạt GTLN bằng \(10 + 4m\).

Với \(m \ge  - \dfrac{{31}}{{32}}\) thì \(10 + 4m \ge \dfrac{{49}}{8}\).

\( \Rightarrow 10 + 4m\) đạt giá trị nhỏ nhất bằng \(\dfrac{{49}}{8}\) khi \(m =  - \dfrac{{31}}{{32}}\).

Khi đó \(a =  - 31,\,\,b = 32 \Rightarrow a + b = 1\) (Không có đáp án).

TH2: \(\dfrac{{31}}{8} + 4m < 0 \le 7 + 4m \Leftrightarrow  - \dfrac{7}{4} \le m \le \dfrac{{ - 31}}{{32}}\).

Khi đó GTLN của hàm số \(y = \left| {2{x^2} - 3x + 4m + 5} \right|\) thuộc \(\left\{ {10 + 4m; - \dfrac{{31}}{8} - 4m} \right\}\).

+ Nếu \(10 + 4m \ge  - \dfrac{{31}}{8} - 4m \Leftrightarrow m \ge  - \dfrac{{111}}{{64}}\).

\( \Rightarrow \max y = 10 + 4m\) đạt GTNN \( \Leftrightarrow m =  - \dfrac{{111}}{{64}}\).

\( \Rightarrow a =  - 111,\,\,b = 64 \Rightarrow a + b =  - 47\).

Chọn C.