Lời giải chi tiết:

Đặt \(a = 1 + x + \dfrac{{{x^2}}}{{2!}} + ... + \dfrac{{{x^{2020}}}}{{2020!}}\), \(b = 1 - x + \dfrac{{{x^2}}}{{2!}} - \dfrac{{{x^3}}}{{3!}} + ... + \dfrac{{{x^{2020}}}}{{2020!}}\).

Ta có:

\(\begin{array}{l}f'\left( x \right) = \left( {1 + x + \dfrac{{{x^2}}}{{2!}} + \dfrac{{{x^3}}}{{3!}} + ... + \dfrac{{{x^{2020}}}}{{2020!}}} \right)\left( {1 - x + \dfrac{{{x^2}}}{{2!}} - \dfrac{{{x^3}}}{{3!}} + ... + \dfrac{{{x^{2020}}}}{{2020!}} - \dfrac{{{x^{2021}}}}{{2021!}}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \left( {1 + x + \dfrac{{{x^2}}}{{2!}} + \dfrac{{{x^3}}}{{3!}} + ... + \dfrac{{{x^{2020}}}}{{2020!}} + \dfrac{{{x^{2021}}}}{{2021!}}} \right)\left( { - 1 + x - \dfrac{{{x^2}}}{{2!}} + \dfrac{{{x^3}}}{{3!}} - ... - \dfrac{{{x^{2020}}}}{{2020!}}} \right)\\ \Rightarrow f'\left( x \right) = a.\left( {b - \dfrac{{{x^{2021}}}}{{2021!}}} \right) - \left( {a + \dfrac{{{x^{2021}}}}{{2021!}}} \right).b\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = ab - a\dfrac{{{x^{2021}}}}{{2021!}} - ab - b\dfrac{{{x^{2021}}}}{{2021!}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =  - \dfrac{{{x^{2021}}}}{{2021!}}\left( {a + b} \right)\\ \Rightarrow f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\a + b = 0 \Leftrightarrow 2\left( {1 + \dfrac{{{x^2}}}{{2!}} + \dfrac{{{x^4}}}{{4!}} + ... + \dfrac{{{x^{2020}}}}{{2020!}}} \right) = 0\,\,\left( * \right)\end{array} \right.\end{array}\)

Dễ thấy phương trình (*) vô nghiệm do \(1 + \dfrac{{{x^2}}}{{2!}} + \dfrac{{{x^4}}}{{4!}} + ... + \dfrac{{{x^{2020}}}}{{2020!}} \ge 1 > 0\,\,\forall x\).

Do đó phương trình \(f'\left( x \right) = 0\) có duy nhất nghiệm \(x = 0\).

Ta có BBT của hàm số \(f\left( x \right)\) trên \(\left[ { - 1;2} \right]\) như sau:

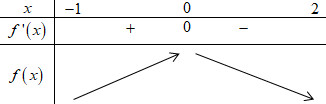
Từ BBT ta thấy \(\mathop {\min }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( 0 \right) = 1\).

Vậy \(a = 1 \in \left( {0;3} \right]\).

Chọn A.