Phương pháp giải:

- Vẽ đồ thị hàm số \(y = \left| {{x^2} - 2x - 3} \right|\)

- Số nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) là số giao điểm của hai đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right).\)

Lời giải chi tiết:

Vẽ đồ thị hàm số \(y = \left| {{x^2} - 2x - 3} \right|\)

+ Vẽ đồ thị hàm số \(y = {x^2} - 2x - 3\) là parabol có đỉnh \(I\left( {1; - 4} \right)\) và đi qua \(\left( {0; - 3} \right),\left( { - 1;0} \right),\left( {3;0} \right)\)

+ Giữ nguyên phần đồ thị phía trên trục hoành, lấy đối xứng phần đồ thị phía dưới \(Ox\) qua \(Ox\), rồi bỏ đi phần đồ thị phía dưới \(Ox\) ta được đồ thị hàm số \(y = \left| {{x^2} - 2x - 3} \right|\)

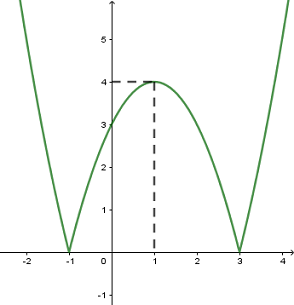
Từ đồ thị hàm số ta có đường thẳng \(y = 2m - 1\) cắt đồ thị tại 4 điểm phân biệt khi :

\(0 < 2m - 1 < 4 \Leftrightarrow \dfrac{1}{2} < m < \dfrac{5}{2}\)

Chọn D.