Câu hỏi
Cho mặt cầu \(\left( S \right)\) có tâm \(I,\) bán kính \(R = \sqrt 3 \) và điểm \(A\) thuộc \(\left( S \right).\) Gọi \(\left( P \right)\) là mặt phẳng đi qua \(A\) và tạo với \(IA\) một góc bằng \(\alpha .\) Biết rằng \(\sin \alpha = \dfrac{1}{3}.\) Tính diện tích của hình tròn có biên là đường tròn giao tuyến của mặt phẳng \(\left( P \right)\) và mặt cầu \(\left( S \right).\)
- A \(\dfrac{\pi }{3}.\)
- B \(\dfrac{{8\pi }}{3}.\)
- C \(\dfrac{\pi }{9}.\)
- D \(\dfrac{{2\sqrt 2 \pi }}{3}.\)
Phương pháp giải:
Công thức tính diện tích đường tròn bán kính \(R\) là: \(S = \pi {R^2}.\)
Lời giải chi tiết:
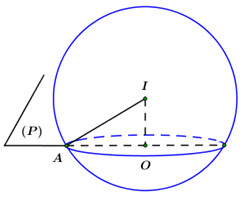
Gọi \(O\) là tâm đường tròn giao tuyến của \(\left( P \right)\) và \(\left( S \right)\)
\( \Rightarrow IO \bot \left( P \right).\)
Khi đó ta có: \(\angle \left( {IA;\,\,\left( P \right)} \right) = \angle \left( {IA,\,\,OA} \right) = \angle IAO.\)
\(\begin{array}{l} \Rightarrow \sin \angle IAO = \dfrac{1}{3} \Leftrightarrow \dfrac{{OI}}{{IA}} = \dfrac{1}{3} \Rightarrow OI = \dfrac{{\sqrt 3 }}{3}.\\ \Rightarrow AO = r = \sqrt {I{A^2} - O{I^2}} = \sqrt {{{\left( {\sqrt 3 } \right)}^2} - {{\left( {\dfrac{{\sqrt 3 }}{3}} \right)}^2}} = \dfrac{{2\sqrt 6 }}{3}\\ \Rightarrow {S_{\left( O \right)}} = \pi {r^2} = \pi {\left( {\dfrac{{2\sqrt 6 }}{3}} \right)^2} = \dfrac{{8\pi }}{3}.\end{array}\)
Chọn B.







