Lời giải chi tiết:

Gọi \(I\) là trung điểm của \(SB\).

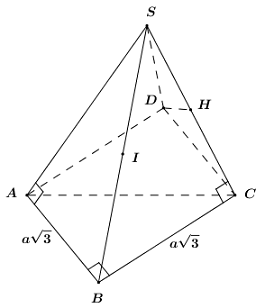
\(\Delta SAB,\,\,\Delta SCB\) vuông tại \(A\) và \(C\) nên \(IA = IC = \dfrac{1}{2}SB = IS = IB\).

\( \Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\).

Gọi \(D\) là đỉnh thứ tư của hình bình hành \(ABCD\). Lại có \(AB \bot BC\) nên \(ABCD\) là hình chữ nhật.

Ta có: \(\left\{ \begin{array}{l}AB \bot BC \Rightarrow AB \bot AD\\AB \bot SA\end{array} \right.\)\( \Rightarrow AB \bot \left( {SAD} \right)\)\( \Rightarrow CD \bot \left( {SAD} \right)\).

\( \Rightarrow CD \bot SD \Rightarrow \Delta SCD\) vuông tại \(D\).

Ta có: \(\left\{ \begin{array}{l}BC \bot CD\\BC \bot SC\end{array} \right. \Rightarrow BC \bot \left( {SCD} \right)\).

Trong \(\left( {SCD} \right)\) kẻ \(DH \bot SC\,\,\left( {H \in SC} \right)\) ta có:  \(\left\{ \begin{array}{l}BC \bot DH\\DH \bot SC\end{array} \right. \Rightarrow DH \bot \left( {SBC} \right)\).

Ta có: \(AD\parallel BC \Rightarrow AD\parallel \left( {SBC} \right)\).

\( \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = d\left( {D;\left( {SBC} \right)} \right) = DH = a\sqrt 2 \).

Áp dụng hệ thức lượng trong tam giác vuông \(SCD\) có:

\(\dfrac{1}{{D{H^2}}} = \dfrac{1}{{S{D^2}}} + \dfrac{1}{{C{D^2}}}\)\( \Rightarrow \dfrac{1}{{2{a^2}}} = \dfrac{1}{{S{D^2}}} + \dfrac{1}{{3{a^2}}}\)\( \Leftrightarrow SD = a\sqrt 6 \).

Áp dụng định lí Pytago trong tam giác vuông \(SCD\) có: \(SC = \sqrt {S{D^2} + C{D^2}} \)\( = \sqrt {6{a^2} + 3{a^2}}  = 3a\).

Áp dụng định lí Pytago trong tam giác vuông \(SBC\) có: \(SB = \sqrt {S{C^2} + B{C^2}} \)\( = \sqrt {9{a^2} + 3{a^2}}  = 2\sqrt 3 a\).

Suy ra bán kính mặt cầu ngoại tiếp chóp \(S.ABC\) là \(R = \dfrac{1}{2}SB = a\sqrt 3 \).

Vậy diện tích mặt cầu ngoại tiếp chóp \(S.ABC\) là \(S = 4\pi {R^2} = 12\pi {a^2}\).

Chọn B.