Phương pháp giải:

- Tính \(AH,\,\,CH\) theo \(R\) và \(\alpha \).

- Thể tích khối nón có đường cao \(h\), bán kính đáy \(r\) là \(V = \dfrac{1}{3}\pi {r^2}h\).

- Sử dụng phương pháp hàm số để tìm GTLN của hàm số.

Lời giải chi tiết:

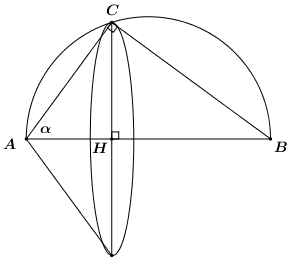
Khi quay tam giác vuông \(ACH\) quanh trục \(AB\) ta nhận được khối nón có chiều cao \(h = AH\), bán kính đáy \(r = CH\).

Ta có \(\angle ACB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) nên \(\Delta ABC\) vuông tại \(C\).

\( \Rightarrow AC = AB.\cos \alpha  = 2R\cos \alpha \).

\( \Rightarrow AH = AC.\cos \alpha  = 2R\cos \alpha .cos\alpha  = 2Rco{s^2}\alpha \), \(CH = AC.\sin \alpha  = 2R\cos \alpha \sin \alpha \).

Thể tích khối nón tạo thành là:

\(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {\left( {2R\cos \alpha sin\alpha } \right)^2}.2R{\cos ^2}\alpha \)

    \( = \dfrac{{8\pi }}{3}{R^3}{\cos ^4}\alpha {\sin ^2}\alpha \)\( = \dfrac{{8\pi {R^3}}}{3}{\cos ^4}\alpha \left( {1 - {{\cos }^2}\alpha } \right)\).

Đặt \(t = {\cos ^2}\alpha \), do \(0 < \alpha  < {90^0}\) nên \(0 < t < 1\).

Khi đó \({\cos ^4}\alpha \left( {1 - {{\cos }^2}\alpha } \right) = {t^2}\left( {1 - t} \right)\).

Xét hàm số \(f\left( t \right) = {t^2}\left( {1 - t} \right) = {t^2} - {t^3}\) với \(0 < t < 1\) ta có: \(f'\left( t \right) = 2t - 3{t^2}\)

\(f'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = \dfrac{2}{3}\end{array} \right.\)

BBT:

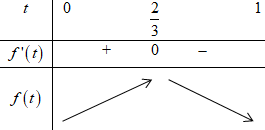
Từ BBT suy ra \({V_{\max }} \Leftrightarrow t = \dfrac{2}{3}\)

\( \Rightarrow {\cos ^2}\alpha  = \dfrac{2}{3}\)\( \Leftrightarrow 1 + {\tan ^2}\alpha  = \dfrac{1}{{{{\cos }^2}\alpha }} = \dfrac{3}{2}\)\( \Leftrightarrow {\tan ^2}\alpha  = \dfrac{1}{2}\)\( \Leftrightarrow \tan \alpha  = \dfrac{1}{{\sqrt 2 }}\) (Do \(0 < \alpha  < {90^0}\) nên \(\tan \alpha  > 0\))

Vậy \(\alpha  = \arctan \dfrac{1}{{\sqrt 2 }}\).

Chọn D.