Câu hỏi
Một vật trang trí bằng pha lê gồm hai hình nón \(\left( {{H_1}} \right)\), \(\left( {{H_2}} \right)\) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng \({r_1},\,\,{h_1}\), \({r_2},\,\,{h_2}\) thỏa mãn \({r_1} = \dfrac{1}{2}{r_2},\,\,{h_1} = \dfrac{1}{2}{h_2}\) (hình vẽ)
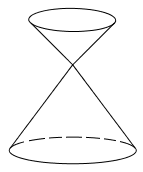
Biết thể tích toàn phần của khối pha lê bằng \(100\,\,c{m^3}\). Tính thể tích của khối \(\left( {{H_1}} \right)\).
- A \(25\,\,c{m^3}\)
- B \(\dfrac{{100}}{9}\,\,c{m^3}\)
- C \(\dfrac{{100}}{3}\,\,c{m^3}\)
- D \(50\,\,c{m^3}\)
Phương pháp giải:
Thể tích khối nón có chiều cao \(h\), bán kính đáy \(R\) là \(V = \dfrac{1}{3}\pi {R^2}h\).
Lời giải chi tiết:
Thể tích của hình nón \(\left( {{H_1}} \right)\) là: \({V_1} = \dfrac{1}{3}\pi r_1^2{h_1}\).
Thể tích của hình nón \(\left( {{H_2}} \right)\) là: \({V_2} = \dfrac{1}{3}\pi r_2^2{h_2} = \dfrac{1}{3}\pi {\left( {2{r_1}} \right)^2}.2{h_1}\)\( = 8.\dfrac{1}{3}\pi r_1^2{h_1} = 8{V_1}\).
\( \Rightarrow {V_1} + 8{V_1} = 100\)\( \Leftrightarrow 9{V_1} = 100\)\( \Leftrightarrow {V_1} = \dfrac{{100}}{9}\).
Chọn B.







