Phương pháp giải:

- Vẽ đồ thị hàm số \(y = f\left( x \right) = \left| {{x^3} - 3\left| x \right| + 1} \right|\).

- Số nghiệm của phương trình \(\left| {{x^3} - 3\left| x \right| + 1} \right| = m - 1\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m - 1\) có tính chất song song với trục hoành.

Lời giải chi tiết:

Ta xét hàm số \(y = {x^3} - 3\left| x \right| + 1 = \left[ \begin{array}{l}{x^3} - 3x + 1\,\,khi\,\,x \ge 0\\{x^3} + 3x + 1\,\,khi\,\,x < 0\end{array} \right.\) .

Khảo sát và vẽ đồ thị hàm số ta được đồ thị như sau:

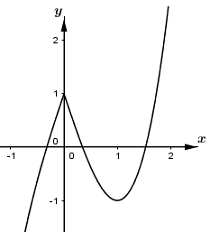
Đồ thị hàm số \(y = f\left( x \right) = \left| {{x^3} - 3\left| x \right| + 1} \right|\) được xác định như sau:

- Từ đồ thị hàm số \(y = {x^3} - 3\left| x \right| + 1\) lấy đối xứng phần đồ thị phía dưới trục hoành qua trục hoành.

- Xóa đi phần đồ thị phía dưới trục hoành.

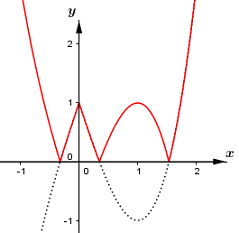
Dựa vào đồ thị hàm số ta thấy để đường thẳng \(y = m - 1\) cắt đồ thị hàm số \(y = f\left( x \right) = \left| {{x^3} - 3\left| x \right| + 1} \right|\) tại 6 điểm phân biệt thì \(0 < m - 1 < 1 \Leftrightarrow 1 < m < 2\) hay \(m \in \left( {1;2} \right)\).

\( \Rightarrow a = 1,\,\,b = 2\). Vậy \(S = {1^2} + {2^2} = 5\).

Chọn C.