Phương pháp giải:

- Biến đổi \(f\left( x \right) = \left| {{x^3} - 3{x^2} + m} \right| = \sqrt {{{\left( {{x^3} - 3{x^2} + m} \right)}^2}} \).

- Tính đạo hàm, tìm điều kiện để phương trình \(f'\left( x \right) = 0\) có 3 nghiệm phân biệt.

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\).

Ta có: \(f\left( x \right) = \left| {{x^3} - 3{x^2} + m} \right| = \sqrt {{{\left( {{x^3} - 3{x^2} + m} \right)}^2}} \).

\(\begin{array}{l} \Rightarrow f'\left( x \right) = \dfrac{{2\left( {{x^3} - 3{x^2} + m} \right)\left( {3{x^2} - 6x} \right)}}{{2\sqrt {{{\left( {{x^3} - 3{x^2} + m} \right)}^2}} }}\\\,\,\,\,\,\,f'\left( x \right) = \dfrac{{\left( {{x^3} - 3{x^2} + m} \right)\left( {3{x^2} - 6x} \right)}}{{\left| {{x^3} - 3{x^2} + m} \right|}}\\\,\,\,\,\,\,f'\left( x \right) = \dfrac{{3x\left( {x - 2} \right)\left( {{x^3} - 3{x^2} + m} \right)}}{{\left| {{x^3} - 3{x^2} + m} \right|}}\end{array}\)

Để hàm số \(f\left( x \right) = \left| {{x^3} - 3{x^2} + m} \right|\) có 3 điểm cực trị thì phương trình \({x^3} - 3{x^2} + m = 0\) hoặc có 1 nghiệm khác \(0;\,\,2\), hoặc có 2 nghiệm phân biệt trong đó có 1 nghiệm bằng 0 hoặc 2, hoặc có 3 nghiệm phân biệt trong đó có 2 nghiệm bằng 0 hoặc 2.

\({x^3} - 3{x^2} + m = 0\) \( \Leftrightarrow -m = {x^3} - 3{x^2} = f\left( x \right)\).

Xét hàm số \(f\left( x \right) = {x^3} - 3{x^2}\) có \(f'\left( x \right) = 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)

BBT:

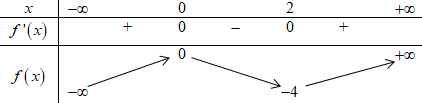
Dựa vào BBT ta thấy:

TH1: Phương trình \({x^3} - 3{x^2} + m = 0\) có 1 nghiệm khác \(0;\,\,2\) \( \Rightarrow \left[ \begin{array}{l} - m > 0\\ - m <  - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < 0\\m > 4\end{array} \right.\).

TH2: Phương trình \({x^3} - 3{x^2} + m = 0\) có 2 nghiệm phân biệt trong đó có 1 nghiệm bằng 0 hoặc 2 \( \Rightarrow \left[ \begin{array}{l} - m = 0\\ - m =  - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 4\end{array} \right.\).

TH3: Phương trình \({x^3} - 3{x^2} + m = 0\) có có 3 nghiệm phân biệt trong đó có 2 nghiệm bằng 0 hoặc 2 \( \Rightarrow m \in \emptyset \).

Suy ra \(\left[ \begin{array}{l}m \le 0\\m \ge 4\end{array} \right.\), kết hợp điều kiện \( \Rightarrow m \in \left[ { - 5;0} \right] \cup \left[ {4;7} \right]\).

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 5; - 4; - 3; - 2; - 1;0;4;5;6;7} \right\}\). Vậy có 10 giá trị của \(m\) thỏa mãn.

Chọn C.