Phương pháp giải:

- Tìm điều kiện để đồ thị hàm số có 3 điểm cực trị.

- Xác định các điểm cực trị của hàm số.

- Sử dụng công thức tính diện tích tam giác \(S = pr\) trong đó \(p\) là nửa chu vi tam giác, \(r\) là bán kính đường tròn nội tiếp tam giác.

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\).

Ta có: \(y' = 4{x^3} - 4mx = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = m\,\,\left( * \right)\end{array} \right.\)

Để đồ thị hàm số có 3 điểm cực trị thì phương trình \(y' = 0\) có 3 nghiệm phân biệt, suy ra phương trình (*) có 2 nghiệm phân biệt khác 0 \( \Rightarrow m > 0\).

Khi đó ta có \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = m\\x = \sqrt m  \Rightarrow y =  - {m^2} + m\\x =  - \sqrt m  \Rightarrow y =  - {m^2} + m\end{array} \right.\)

\( \Rightarrow \) Đồ thị hàm số có 3 điểm cực trị \(A\left( {0;m} \right)\), \(B\left( {\sqrt m ; - {m^2} + m} \right)\), \(C\left( { - \sqrt m ; - {m^2} + m} \right)\).

Dễ nhận thấy \(\Delta ABC\) cân  tại \(A\).

Phương trình đường thẳng \(BC\) là: \(y =  - {m^2} + m \Leftrightarrow y + {m^2} - m = 0\).

\( \Rightarrow d\left( {A;BC} \right) = \dfrac{{\left| {m + {m^2} - m} \right|}}{{\sqrt {{0^2} + {1^2}} }} = {m^2}\); \(BC = \sqrt {{{\left( { - 2\sqrt m } \right)}^2}}  = 2\sqrt m \).

\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}d\left( {A;BC} \right).BC\) \( = \dfrac{1}{2}.{m^2}.2\sqrt m  = \sqrt {{m^5}} \).

Gọi \(r\) là bán kính đường tròn nội tiếp tam giác \(ABC\), \(p\) là nửa chu vi tam giác \(ABC\).

Ta có: \(\left\{ \begin{array}{l}AB = AC = \sqrt {{{\left( {\sqrt m } \right)}^2} + {{\left( { - {m^2}} \right)}^2}}  = \sqrt {{m^4} + m} \\BC = 2\sqrt m \end{array} \right.\)\( \Rightarrow p = \sqrt {{m^4} + m}  + \sqrt m \).

\( \Rightarrow r = \dfrac{{{S_{ABC}}}}{p} = \dfrac{{\sqrt {{m^5}} }}{{\sqrt {{m^4} + m}  + \sqrt m }}\).

Theo bài ra ta có:  \(\dfrac{{\sqrt {{m^5}} }}{{\sqrt {{m^4} + m}  + \sqrt m }} > 1\).

Do \(m > 0\) nên loại đáp án A và C.

Chọn \(m = 3\):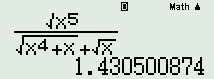 \( > 1\), do đó \(m = 3\) thỏa mãn.

Vậy \(m > 2\) là đáp án đúng.

Chọn B.