Câu hỏi
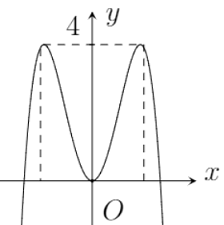
Hình vẽ dưới đây là đồ thị của hàm số \(y = - {x^4} + 4{x^2}\). Với giá trị nào của \(m\) thì phương trình \({x^4} - 4{x^2} + m - 2 = 0\) có bốn nghiệm phân biệt?
- A \(0 \le m < 4\)
- B \(0 < m < 4\)
- C \(0 \le m \le 6\)
- D \(2 < m < 6\)
Phương pháp giải:
Số nghiệm của phương trình \(f\left( x \right) = m\) chính bằng số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\) có tính chất song song với trục hoành.
Lời giải chi tiết:
\({x^4} - 4{x^2} + m - 2 = 0\)\( \Leftrightarrow m - 2 = - {x^4} + 4{x^2}\) (*).
\( \Rightarrow \) Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số \(y = - {x^4} + 4{x^2}\) và đường thẳng \(y = m - 2\) song song với trục hoành.
Dựa vào đồ thị hàm số ta thấy phương trình (*) có 4 nghiệm \( \Leftrightarrow \) đường thẳng \(y = m - 2\) cắt đồ thị hàm số \(y = - {x^4} + 4{x^2}\) tại 4 điểm phân biệt \( \Rightarrow 0 < m -2 < 4\) \( \Leftrightarrow 2 < m < 6\).
Chọn D.
Câu hỏi trước
