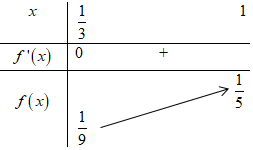Câu hỏi
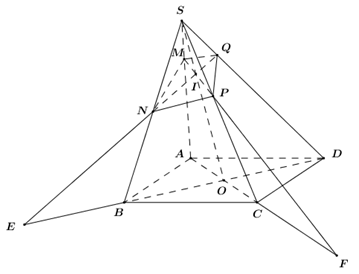
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(N\) là trung điểm của \(SB\), \(Q\) là điểm thuộc cạnh \(SD\) sao cho \(DQ = 3SQ\). Mặt phẳng \(\left( \alpha \right)\) đi qua \(NQ\) và cắt các cạnh \(SA,\,\,SC\) lần lượt tại \(M,\,\,P\). Giá trị nhỏ nhất của tỉ số \(\frac{{{V_{S.MNPQ}}}}{{{V_{S.ABCD}}}}\) bằng:
- A \(\frac{3}{{20}}\)
- B \(\frac{1}{{30}}\)
- C \(\frac{1}{{60}}\)
- D \(\frac{1}{{24}}\)
Lời giải chi tiết:
Gọi \(O = AC \cap BD\).
Lấy \(M \in SA\), trong \(\left( {SBD} \right)\) gọi \(I = NQ \cap SO\). Trong \(\left( {SAC} \right)\) kéo dài \(MI\) cắt \(SC\) tại \(P\).
Đặt \(\frac{{SM}}{{SA}} = x,\,\,\frac{{SP}}{{SC}} = y\) (Giả sử \(0 < x < y \le 1\)).
Gọi \(NQ \cap BD = E\), \(MP \cap AC = F\).
Áp dụng định lí Menelaus ta có:
\(\frac{{NS}}{{NB}}.\frac{{EB}}{{ED}}.\frac{{QD}}{{QS}} = 1\) \( \Rightarrow 1.\frac{{EB}}{{ED}}.3 = 1 \Leftrightarrow \frac{{EB}}{{ED}} = \frac{1}{3}\)\( \Rightarrow EB = OB = OD\) \( \Rightarrow \frac{{EB}}{{EO}} = \frac{1}{2}\).
\(\frac{{NS}}{{NB}}.\frac{{EB}}{{EO}}.\frac{{IO}}{{IS}} = 1\) \( \Rightarrow 1.\frac{1}{2}.\frac{{IO}}{{IS}} = 1 \Leftrightarrow \frac{{IO}}{{IS}} = 2\).
\(\frac{{MS}}{{MA}}.\frac{{FA}}{{FO}}.\frac{{IO}}{{IS}} = 1\) \( \Rightarrow \frac{x}{{1 - x}}.\frac{{FA}}{{FO}}.2 = 1 \Leftrightarrow \frac{{FA}}{{FO}} = \frac{{1 - x}}{{2x}}\)\( \Leftrightarrow \frac{{FO + OA}}{{FO}} = \frac{{1 - x}}{{2x}}\).
\(\frac{{PS}}{{PC}}.\frac{{FC}}{{FO}}.\frac{{IO}}{{IS}} = 1\) \( \Rightarrow \frac{y}{{1 - y}}.\frac{{FC}}{{FO}}.2 = 1 \Leftrightarrow \frac{{FC}}{{FO}} = \frac{{1 - y}}{{2y}}\) \( \Leftrightarrow \frac{{FO - OA}}{{FO}} = \frac{{1 - y}}{{2y}}\).
\(\begin{array}{l} \Rightarrow \frac{{FO + OA}}{{FO}} + \frac{{FO - OA}}{{FO}} = \frac{{1 - x}}{{2x}} + \frac{{1 - y}}{{2y}}\\ \Rightarrow 2 = \frac{{1 - x}}{{2x}} + \frac{{1 - y}}{{2y}} \Leftrightarrow 2 = \frac{{y\left( {1 - x} \right) + x\left( {1 - y} \right)}}{{2xy}}\\ \Leftrightarrow 4xy = y - xy + x - xy = x + y - 2xy\\ \Leftrightarrow x + y = 6xy\,\,\,\left( * \right) \Leftrightarrow \frac{1}{x} + \frac{1}{y} = 6\end{array}\)
Không mất tính tổng quát, ta giả sử \(0 < x \le y \le 1 \Leftrightarrow \frac{1}{x} \ge \frac{1}{y}\), khi đó ta có:
\(\frac{1}{y} + \frac{1}{y} \le \frac{1}{x} + \frac{1}{y} = 6 \Leftrightarrow \frac{2}{y} \le 6 \Leftrightarrow y \ge \frac{1}{3}\).
Đặt \(k = \frac{{{V_{S.MNPQ}}}}{{{V_{S.ABCD}}}}\), ta có:
\(\frac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SB}}.\frac{{SP}}{{SC}} = \frac{{xy}}{2}\) \( \Rightarrow {V_{S.MNP}} = \frac{{xy}}{4}{V_{S.ABCD}}\).
\(\frac{{{V_{S.MQP}}}}{{{V_{S.ADC}}}} = \frac{{SM}}{{SA}}.\frac{{SQ}}{{SD}}.\frac{{SP}}{{SC}} = \frac{{xy}}{4}\) \( \Rightarrow {V_{S.MNP}} = \frac{{xy}}{8}{V_{S.ABCD}}\).
\( \Rightarrow \frac{{{V_{SMNPQ}}}}{{{V_{S.ABCD}}}} = \frac{{xy}}{4} + \frac{{xy}}{8} = \frac{{3xy}}{8} = k\).
Từ (*) ta có: \(x\left( {6y - 1} \right) = y \Leftrightarrow x = \frac{y}{{6y - 1}}\,\,\left( {y \ge \frac{1}{3}} \right)\) \( \Rightarrow k = \frac{3}{8}\frac{{{y^2}}}{{6y - 1}}\)
Xét hàm số \(f\left( x \right) = \frac{{{y^2}}}{{6y - 1}}\), với \(y \ge \frac{1}{3}\) ta có:
\(f'\left( y \right) = \frac{{2y\left( {6y - 1} \right) - 6{y^2}}}{{{{\left( {6y - 1} \right)}^2}}} = \frac{{6{y^2} - 2y}}{{{{\left( {6y - 1} \right)}^2}}}\) ; \(f'\left( y \right) = 0 \Leftrightarrow 6{y^2} - 2y = 0 \Leftrightarrow \left[ \begin{array}{l}y = 0\\y = \frac{1}{3}\end{array} \right.\)
BBT:
Vậy \({k_{\min }} = \frac{3}{8}.\frac{1}{9} = \frac{1}{{24}}\).
Chọn D.