Câu hỏi
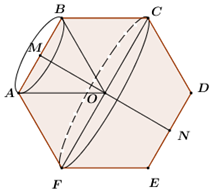
Trong mặt phẳng cho hình lục giác đều \(ABCDEF\) có bán kính đường tròn ngoại tiếp bằng \(a\). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AB,\,\,DE\). Tính thể tích hình nón tròn xoay sinh ra khi cho lục giác quay quanh trục là đường thẳng \(MN\).
- A \(\frac{{7\sqrt 3 \pi {a^3}}}{4}\)
- B \(\frac{{7\sqrt 3 \pi {a^3}}}{{18}}\)
- C \(\frac{{7\sqrt 3 \pi {a^3}}}{{24}}\)
- D \(\frac{{7\sqrt 3 \pi {a^3}}}{{12}}\)
Phương pháp giải:
Khối nón cụt có đáy lớn \(R\), đáy nhỏ \(r\), chiều cao \(h\) có thể tích \(V = \frac{1}{3}\pi h\left( {{R^2} + {r^2} + Rr} \right)\).
Lời giải chi tiết:
Do \(ABCDEF\) là lục giác đều nên \(\Delta OAB\) đều.
Lại có \(OA = OB = a\) nên tam giác \(ABC\) đều cạnh \(a\) \( \Rightarrow AB = a\) và trung tuyến \(OM\) đồng thời là đường cao và \(OM = \frac{{a\sqrt 3 }}{2}\).
Khi xoay hình lục giác đều quanh đường thẳng \(MN\), ta được khối tròn xoay có thể tích bằng 2 lần thể tích hình nón cụt có đáy lớn \(R = OF = a\), đáy nhỏ \(r = AM = \frac{a}{2}\), đường cao \(h = OM = \frac{{a\sqrt 3 }}{2}\).
Vậy thể tích khối tròn xoay cần tính là:
\(V = 2.\frac{1}{3}\pi h\left( {{R^2} + {r^2} + Rr} \right)\)\( = \frac{{2\pi }}{3}.\frac{{a\sqrt 3 }}{2}\left( {{a^2} + \frac{{{a^2}}}{4} + \frac{{{a^2}}}{2}} \right) = \frac{{7\sqrt 3 \pi {a^3}}}{{12}}\).
Chọn D.