Câu hỏi
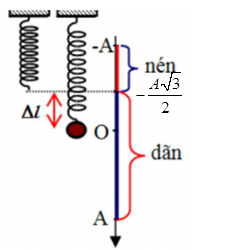
Một con lắc lò xo treo thẳng đứng dao động điều hòa với biên độ \(A = \dfrac{{2\sqrt 3 }}{3}\Delta {l_0}\) (\(\Delta {l_0}\) là độ dãn của lò xo khi vật ở vị trí cân bằng). Tỉ số giữa thời gian lò xo nén và lò xo dãn trong 1 chu kỳ dao động là
- A \(\dfrac{1}{3}.\)
- B \(\dfrac{1}{5}.\)
- C \(3.\)
- D \(5.\)
Phương pháp giải:
Sử dụng trục thời gian suy ra từ vòng tròn
Lời giải chi tiết:
Ta có: \(A = \dfrac{{2\sqrt 3 }}{3}\Delta {l_0} \Rightarrow \Delta {l_0} = \dfrac{{A\sqrt 3 }}{2}\)
Chọn chiều dương hướng xuống, ta có:
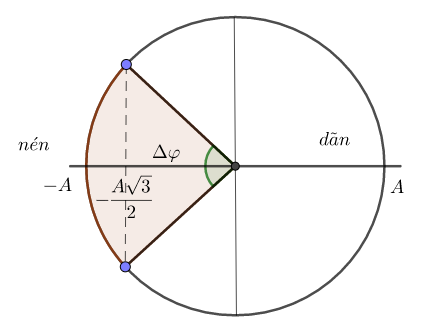
+ Thời gian lò xo nén trong 1 chu kì: \({t_{nen}} = 2\dfrac{T}{{12}} = \dfrac{T}{6}\)
+ Thời gian lò xo dãn trong 1 chu kì: \({t_{dan}} = T - {t_{nen}} = T - \dfrac{T}{6} = \dfrac{{5T}}{6}\)
\( \Rightarrow \dfrac{{{t_{nen}}}}{{{t_{dan}}}} = \dfrac{{\dfrac{T}{6}}}{{\dfrac{{5T}}{6}}} = \dfrac{1}{5}\)
Chọn B
Câu hỏi trước
