Câu hỏi
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\), có 3 cực trị và có đồ thị như hình vẽ.
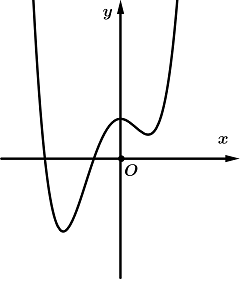
Tìm số điểm cực trị của hàm số \(y = f\left( {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}} \right)\).
- A \(3.\)
- B \(0.\)
- C \(1.\)
- D \(2.\)
Phương pháp giải:
Tính \(\left[ {f\left( {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}} \right)} \right]'\) và tìm số nghiệm bội lẻ, từ đó suy ra số cực trị.
Lời giải chi tiết:
Ta có:
\(g'\left( x \right) = \left[ {f\left( {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}} \right)} \right]' = \left[ {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}} \right]'.f'\left( {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}} \right)\)\( = - \dfrac{2}{{{{\left( {x - 1} \right)}^3}}}.f'\left( {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}} \right)\)
\(g'\left( x \right) = 0 \Leftrightarrow f'\left( {\dfrac{1}{{{{\left( {x - 1} \right)}^2}}}} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}\dfrac{1}{{{{\left( {x - 1} \right)}^2}}} = {x_1} < 0\left( {VN} \right)\\\dfrac{1}{{{{\left( {x - 1} \right)}^2}}} = {x_2} = 0\left( {VN} \right)\\\dfrac{1}{{{{\left( {x - 1} \right)}^2}}} = {x_3} > 0\end{array} \right.\)\( \Leftrightarrow x - 1 = \pm \sqrt {\dfrac{1}{{{x_3}}}} \Leftrightarrow x = 1 \pm \sqrt {\dfrac{1}{{{x_3}}}} \) (nghiệm đơn)
Vậy hàm số đã cho có \(2\) điểm cực trị.
Chọn D.







