Môn Lý - Lớp 12
50 bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ Frenen mức độ vận dụng cao
Câu hỏi
Cho D1, D2 và D3 là ba dao động điều hòa cùng phương, cùng tần số. Dao động tổng hợp của D1 và D2 có phương trình \({x_{12}} = 5\sqrt 6 \cos \left( {\omega t - \pi } \right)\,\,\left( {cm} \right)\). Dao động tổng hợp của D2 và D3 có phương trình \({x_{23}} = 5\cos \left( {\omega t - \dfrac{\pi }{2}} \right)\,\,\left( {cm} \right)\). Dao động D1 ngược pha với dao động D3. Biên độ của dao động D2 có giá trị nhỏ nhất là
- A 6,4 cm
- B 4,6 cm
- C 6,8 cm
- D 8,6 cm
Phương pháp giải:
Sử dụng giản đồ vecto và hệ thức lượng trong tam giác vuông.
Lời giải chi tiết:
Ta có giản đồ vecto:
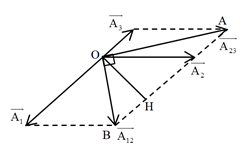
Nhận xét: \({A_{2\min }} \Leftrightarrow \overrightarrow {{A_2}} \equiv \overrightarrow {OH} \)
Xét Δ OAB vuông tại O, ta có:
\(\begin{array}{l}\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} \Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{{{\left( {5\sqrt 6 } \right)}^2}}} + \dfrac{1}{{{5^2}}}\\ \Rightarrow OH = 4,629\,\,\left( {cm} \right) \approx 4,6\,\,\left( {cm} \right)\\ \Rightarrow {A_{2\min }} = OH = 4,6\,\,\left( {cm} \right)\end{array}\)
Chọn B.
Câu hỏi trước
