Câu hỏi
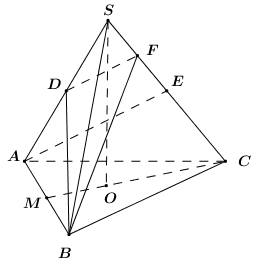
Cho hình chóp tam giác đều \(S.ABC\) có \(SA = 2\). Gọi \(D,\,\,E\) lần lượt là trung của cạnh \(SA,\,\,SC\). Tính thể tích khối chóp \(S.ABC\) biết \(BD \bot AE\).
- A \(\frac{{4\sqrt {21} }}{9}\)
- B \(\frac{{4\sqrt {21} }}{7}\)
- C \(\frac{{4\sqrt {21} }}{3}\)
- D \(\frac{{4\sqrt {21} }}{{27}}\)
Phương pháp giải:
- Gọi \(F\) là trung điểm của \(SE\), suy ra \(DF \bot BD\).
- Đặt \(AB = BC = CA = x\), tính \(BD,\,\,DF,\,\,BF\).
- Áp dụng định lí Pytago trong tam giác vuông tìm \(x\).
- Tính chiều cao và diện tích đáy của hình chóp, áp dụng công thức tính thể tích khối chóp \(V = \frac{1}{3}{S_{day}}.h\).
Lời giải chi tiết:
Đặt \(AB = BC = CA = x\).
Gọi \(F\) là trung điểm của \(SE\) ta có \(DF\) là đường trung bình của tam giác \(SAE\) nên \(DF\parallel AE\).
Mà \(AE \bot BD\) nên \(DF \bot BD \Rightarrow \Delta BDF\) vuông tại \(D\).
Xét tam giác \(SAB\) có: \(B{D^2} = \frac{{A{B^2} + S{B^2}}}{2} - \frac{{S{A^2}}}{4}\)\( = \frac{{{x^2} + 4}}{2} - \frac{4}{4}\) \( = \frac{{{x^2}}}{2} + 1\).
CMTT ta có \(A{E^2} = \frac{{{x^2}}}{2} + 1 \Rightarrow D{F^2} = \frac{{{x^2}}}{8} + \frac{1}{4}\).
Xét tam giác \(SBC\) có:
\(\cos \angle BSC = \frac{{S{B^2} + S{C^2} - B{C^2}}}{{2SB.SC}}\) \( = \frac{{4 + 4 - {x^2}}}{{2.2.2}} = 1 - \frac{{{x^2}}}{8}\).
Xét tam giác \(SBF\) có:
\(\begin{array}{l}B{F^2} = S{B^2} + S{F^2} - 2SB.SF.\cos \angle BSC\\\,\,\,\,\,\,\,\,\,\,\, = {2^2} + {\left( {\frac{1}{2}} \right)^2} - 2.2.\frac{1}{2}\left( {1 - \frac{{{x^2}}}{8}} \right)\\\,\,\,\,\,\,\,\,\,\,\, = \frac{{17}}{4} - 2 + \frac{{{x^2}}}{4} = \frac{9}{4} + \frac{{{x^2}}}{4}\end{array}\)
Áp dụng định lí Pytago trong tam giác vuông \(BDF\) ta có:
\(\begin{array}{l}\,\,\,\,\,\,B{F^2} = B{D^2} + D{F^2}\\ \Leftrightarrow \frac{9}{4} + \frac{{{x^2}}}{4} = \frac{{{x^2}}}{2} + 1 + \frac{{{x^2}}}{8} + \frac{1}{4}\\ \Leftrightarrow \frac{{3{x^2}}}{8} = 1 \Leftrightarrow x = \frac{{2\sqrt 6 }}{3}\end{array}\)
Gọi \(O\) là trọng tâm tam giác \(ABC \Rightarrow SO \bot \left( {ABC} \right)\).
Gọi \(M\) là trung điểm của \(AB\) ta có: \(CM = \frac{{2\sqrt 6 }}{3}.\frac{{\sqrt 3 }}{2} = \sqrt 2 \) \( \Rightarrow CO = \frac{2}{3}CM = \frac{{2\sqrt 2 }}{3}\).
Áp dụng định lí Pytago trong tam giác vuông \(SOC\) có:
\(SO = \sqrt {S{C^2} - C{O^2}} \) \( = \sqrt {{2^2} - {{\left( {\frac{{2\sqrt 2 }}{3}} \right)}^2}} = \frac{{2\sqrt 7 }}{3}\).
Tam giác \(ABC\) đều cạnh \(\frac{{2\sqrt 6 }}{3}\) nên \({S_{\Delta ABC}} = {\left( {\frac{{2\sqrt 6 }}{3}} \right)^2}\frac{{\sqrt 3 }}{4} = \frac{{2\sqrt 3 }}{3}\).
Vậy \({V_{S.ABC}} = \frac{1}{3}SO.{S_{\Delta ABC}}\) \( = \frac{1}{3}.\frac{{2\sqrt 7 }}{3}.\frac{{2\sqrt 3 }}{3}\)\( = \frac{{4\sqrt {21} }}{{27}}\).
Chọn D.