Câu hỏi
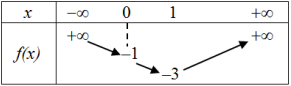
Cho hàm số bậc hai \(f\left( x \right) = a{x^2} + bx + c\) có bảng biến thiên như hình vẽ dưới. Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 2018;2018} \right]\) để phương trình \(f\left( x \right) - m - 4 = 0\) có một nghiệm dương duy nhất.
- A \(2026\)
- B \(2020\)
- C \(2025\)
- D \(2024\)
Phương pháp giải:
Dựa vào bảng biến thiên để biện luận số nghiệm của phương trình.
Lời giải chi tiết:
Từ bảng biến thiên suy ra phương trình \(f\left( x \right) = m + 4\) có nghiệm dương duy nhất \( \Leftrightarrow m + 4 \ge - 1 \Leftrightarrow m \ge - 5.\)
Mà \(m \in \left[ { - 2018;\,\,2018} \right] \Rightarrow m \in \left[ { - 5;\,\,2018} \right]\)
Vậy có \(2024\) giá trị nguyên của \(m\) thỏa mãn.
Chọn D.
Câu hỏi trước
