Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số như hình.
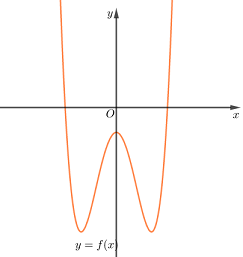
Hàm số \(y = \left| {f\left( {x + 2018} \right)} \right|\) có bao nhiêu điểm cực trị?
- A \(5\)
- B \(2\)
- C \(1\)
- D \(3\)
Phương pháp giải:
Dùng phép suy đồ thị, từ đồ thị hàm số \(y = f\left( x \right)\), vẽ đồ thị hàm số \(g\left( x \right) = f\left( {x + 2018} \right)\) bằng cách dịch chuyển đồ thị \(y = f\left( x \right)\) sang bên trái 2018 đơn vị.
Vẽ đồ thị hàm số \(h\left( x \right) = \left| {g\left( x \right)} \right|\) bằng cách lấy đối xứng phần đồ thị \(g\left( x \right)\) phía dưới trục hoành qua trục hoành rồi bỏ đi phần đồ thị phía dưới trục hoành đó.
Từ đồ thị hàm số \(y = h\left( x \right)\) suy ra số điểm cực trị của hàm \(y = h\left( x \right) = \left| {f\left( {x + 2018} \right)} \right|\)
Lời giải chi tiết:
Từ đồ thị hàm số đã cho, ta vẽ được các hàm số sau:
Vẽ đồ thị hàm số \(g\left( x \right) = f\left( {x + 2018} \right)\) bằng cách dịch chuyển đồ thị \(y = f\left( x \right)\) sang bên trái 2018 đơn vị.
Lấy đối xứng phần đồ thị \(g\left( x \right)\) phía dưới trục hoành qua trục hoành rồi bỏ đi phần đồ thị phía dưới trục hoành đó ta được đồ thị của hàm số \(y = h\left( x \right) = \left| {g\left( x \right)} \right| = \left| {f\left( {x + 2018} \right)} \right|\) như hình vẽ dưới đây
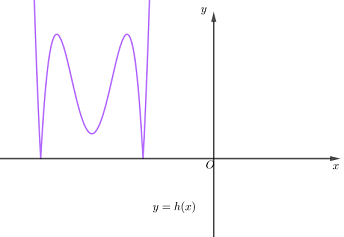
Từ đồ thị hàm số \(y = h\left( x \right)\) ta thấy đồ thị hàm số \(y = \left| {f\left( {x + 218} \right)} \right|\) có 5 điểm cực trị
Chọn A.







