Phương pháp giải:

Mặt cầu tiếp xúc với 12 cạnh của hình lập phương, có tâm là tâm của hình lập phương, tiếp xúc với mỗi cạnh của hình lập phương tại trung điểm của nó.

Tính bán kính của mặt cầu trên.

Diện tích xung quanh của mặt cầu có bán kính \(R\) được tính bởi công thức \({S_{xq}} = 4\pi {R^2}\)

Lời giải chi tiết:

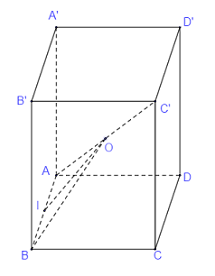
Gọi hình lập phương đã cho là \(ABCD.A'B'C'D'\), \(O\) là giao điểm 2 đường chéo lớn hay \(O\) là tâm của hình lập phương.

Gọi \(I\) là trung điểm \(AB\)

Mặt cầu tiếp xúc với 12 cạnh của hình lập phương, có tâm là tâm của hình lập phương, tiếp xúc với mỗi cạnh của hình lập phương tại trung điểm của nó. Suy ra mặt cầu tiếp xúc với 12 cạnh của lập phương có tâm là \(O\) và bán kính \(R = OI\)

\(I\) là trung điểm \(AB\) nên \(IA = IB = 2\left( {cm} \right)\)

Ta có:

    \(AC' = \sqrt {AA{'^2} + A'C{'^2}}  = \sqrt {AA{'^2} + A'B{'^2} + B'C{'^2}}  = \sqrt 3 .4 = 4\sqrt 3 \)    \( \Rightarrow AO = \dfrac{1}{2}AC' = 2\sqrt 3 \)

    \(OI \bot AB \Rightarrow OI = \sqrt {O{A^2} - A{I^2}}  = \sqrt {{{\left( {2\sqrt 3 } \right)}^2} - {2^2}}  = 2\sqrt 2 \left( {cm} \right)\)

Suy ra diện tích xung quanh của mặt cầu trên là:

              \({S_{xq}} = 4\pi {R^2} = 4\pi .O{I^2} = 32\pi \left( {c{m^2}} \right)\)

Chọn A