Câu hỏi
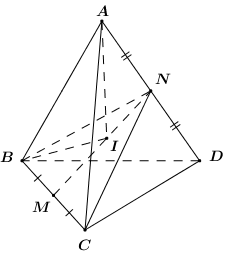
Cho tứ diện \(ABCD\) có \(AB = BC = CD = 2,\) \(AC = BD = 1\), \(AD = \sqrt 3 \). Tính bán kính của mặt cầu ngoại tiếp tứ diện đã cho.
- A \(\frac{{\sqrt 7 }}{3}\)
- B \(\frac{{\sqrt {39} }}{6}\)
- C \(\frac{{2\sqrt 3 }}{3}\)
- D \(1\)
Lời giải chi tiết:
Gọi \(M,\,\,N\) lần lượt là trung điểm của \(BC\) và \(AD\).
Xét \(\Delta ADB\) và \(\Delta DAC\) có:
\(\begin{array}{l}AD\,\,chung\\BD = AC = 1\\AB = CD = 2\end{array}\)
\( \Rightarrow \Delta ADB = \Delta DAC\,\,\,\left( {c.c.c} \right)\) \( \Rightarrow \angle DAB = \angle ADC\) (2 góc tương ứng) hay \(\angle NAB = \angle NDC\).
Xét \(\Delta ABN\) và \(\Delta DCN\) có:
\(\begin{array}{l}AN = DN\,\,\left( {gt} \right);\\\angle NAB = \angle NDC\,\,\,\left( {cmt} \right);\\AB = CD = 2\,\,\left( {gt} \right)\end{array}\)
\( \Rightarrow \Delta ABN = \Delta DCN\,\,\left( {c.g.c} \right)\) \( \Rightarrow BN = CN\).
\( \Rightarrow \Delta NBC\) cân tại \(N\).
\( \Rightarrow \) Trung tuyến \(MN\) đồng thời là trung trực.
CMTT ta có \(MN\) là trung trực của \(AD\).
Lấy \(I \in MN \Rightarrow \left\{ \begin{array}{l}IA = ID\\IB = IC\end{array} \right.\).
Giả sử điểm \(I\) thỏa mãn \(IA = IB\), khi đó \(IA = IB = IC = ID = R\) hay \(I\) chính là tâm mặt cầu ngoại tiếp tứ diện \(ABCD\).
Xét \(\Delta ABD\) có: \(B{N^2} = \frac{{A{B^2} + B{D^2}}}{2} - \frac{{A{D^2}}}{4}\) \( = \frac{{{2^2} + {1^2}}}{2} - \frac{{{{\left( {\sqrt 3 } \right)}^2}}}{4} = \frac{7}{4}\) \( \Rightarrow BN = \frac{{\sqrt 7 }}{2}\).
Áp dụng định lí Pytago trong tam giác vuông \(BMN\) có:
\(M{N^2} = B{N^2} - B{M^2}\)\( = \frac{7}{4} - 1 = \frac{3}{4}\) \( \Rightarrow MN = \frac{{\sqrt 3 }}{2}\).
Áp dụng định lí Pytago trong các tam giác vuông \(IBM\) và \(IAN\) có:
\(\begin{array}{l}IM = \sqrt {I{B^2} - B{M^2}} = \sqrt {{R^2} - 1} \\IN = \sqrt {I{A^2} - A{N^2}} = \sqrt {{R^2} - \frac{3}{4}} \end{array}\)
Lại có \(MN = IM + IN\)\( \Rightarrow \frac{{\sqrt 3 }}{2} = \sqrt {{R^2} - 1} + \sqrt {{R^2} - \frac{3}{4}} \).
Sử dụng MTCT, CALC 4 đáp án đã cho ta tìm được \(R = \frac{{\sqrt {39} }}{6}\).
Chọn B.