Phương pháp giải:

Tìm bán kính của đường tròn ngoại tiếp tam giác đáy

Diện tích xung quanh của hình nón được tính bởi công thức   \({S_{xq}} = \pi rl\)(với \(r:\) bán kính đáy,  \(l:\) đường sinh.)

Lời giải chi tiết:

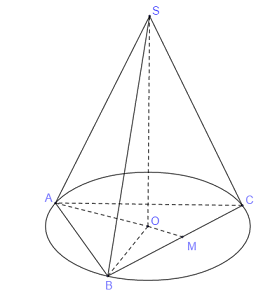
Tứ diện đều \(S.ABC\) có đỉnh \(S\) trùng với đỉnh của hình nón và tam giác \(ABC\) nội tiếp đường tròn đáy của hình nón nên đường sinh của hình nón bằng  cạnh bên \(SA\).

\(S.ABC\) là tứ diện đều nên \(SA = SB = SC = AB = BC = CA = 3\left( {cm} \right)\)

Tam giác \(ABC\) đều nên gọi \(O\) là trọng tâm của tam giác thì \(O\) cũng là tâm đường tròn ngoại tiếp tam giác \(ABC\).

Gọi \(M\) là trung điểm \(BC\) thì \(A,O,M\) thẳng hàng và \(AO = \dfrac{2}{3}AM\)

Ta có :

                   \(\begin{array}{l}A{M^2} + B{M^2} = A{B^2}\\ \Leftrightarrow A{M^2} + {\left( {\dfrac{3}{2}} \right)^2} = {3^2}\\ \Rightarrow AM = \dfrac{{3\sqrt 3 }}{2} \Rightarrow AO = \dfrac{2}{3}AM = \sqrt 3 \left( {cm} \right)\end{array}\)

Suy ra diện tích xung quanh của hình nón là :

     \(V = \pi rl = \pi .AO.SA = \pi .\sqrt 3 a.3a = 3\sqrt 3 \pi {a^2}\left( {c{m^2}} \right)\)

Chọn C.