Câu hỏi
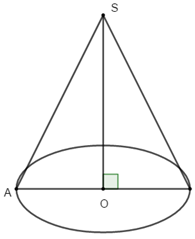
Cho hình nón tròn xoay có đường sinh bằng \(a\sqrt 2 \) và góc giữa đường sinh và mặt phẳng đó bằng \(60^\circ .\) Tính diện tích xung quanh \({S_{xq}}\) của hình nón và thể tích V của khối nón.
- A \({S_{xq}} = \pi {a^2};\,\,V = \frac{{\sqrt 6 }}{2}{a^3}\)
- B \({S_{xq}} = 2\pi {a^2};\,\,V = \frac{{\sqrt 3 }}{2}{a^3}\)
- C \({S_{xq}} = 2\pi {a^2};\,\,V = \frac{{\sqrt 6 }}{2}{a^3}\)
- D \({S_{xq}} = \pi {a^2};\,\,V = \frac{{\sqrt 3 }}{2}{a^3}\)
Phương pháp giải:
Sử dụng công thức lượng giác tring tam giác.
Áp dụng công thức tính diện tích xung quanh và thể tích.
Lời giải chi tiết:
\(\Delta SAO\) vuông tại O; có \(SA = a\sqrt 2 ;\angle SAO = 60^\circ \Rightarrow \left\{ \begin{array}{l}R = AO = \cos 60^\circ .SA = \frac{{a\sqrt 2 }}{2}\\h = SO = \sin 60^\circ .SA = \frac{{a\sqrt 6 }}{2}\end{array} \right.\)
Khi đó \({S_{xq}} = \pi Rl = \pi {a^2}.;\,\,V = \pi Rh = \frac{{\sqrt 6 }}{2}{a^{3.}}\)
Chọn A.
Câu hỏi trước
