Câu hỏi
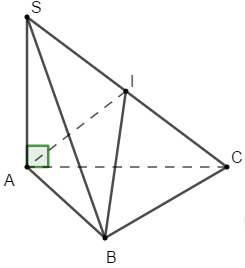
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B với \(AB = 3a,BC = 4a,SA \bot \left( {ABC} \right),\)cạnh bên SC tạo với đáy góc \(60^\circ .\) Thể tích khối cầu ngoại tiếp tứ diện S.ABC là
- A \(V = \frac{{50\pi {a^3}}}{3}.\)
- B \(V = \frac{{500\pi {a^3}}}{3}.\)
- C \(V = \frac{{\pi {a^3}}}{3}.\)
- D \(V = \frac{{5\pi {a^3}}}{3}.\)
Phương pháp giải:
Tìm tâm mặt cầu ngoại tiếp tứ diện.
Tính bán kính mặt cầu rồi tính thể tích dựa theo công thức \(V = \frac{4}{3}\pi {R^3}.\)
Lời giải chi tiết:
Gọi I là trung điểm của SC.
Ta có \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\)vuông tại A
Do đó \(IA = IS = IC\)
Mặt khác \(BC \bot AB;BC \bot SA \Rightarrow BC \bot SB \Rightarrow \Delta SBC\) vuông tại B.
Mà I là trung điểm của SC nên \(IS = IB = IC\)
Suy ra I là tâm mặt cầu ngoại tiếp tứ diện S.ABC.
+)\(\Delta ABC\) vuông tại B; có \(AB = 3;BC = 4\)\( \Rightarrow AC = 5\)
+)\(\Delta SAC\) vuông tại A có \(AC = 5;\angle SCA = 60^\circ \Rightarrow SC = \frac{1}{{{\rm{cos60}}^\circ {\rm{.}}AC}} = 10\)
Suy ra \(R = 5 \Rightarrow V = \frac{4}{3}\pi {R^3} = \frac{{500\pi {a^3}}}{3}.\)
Chọn B.