Phương pháp giải:

Tìm đạo hàm của hàm số.

Lập bảng biến thiên để tìm gía trị lớn nhất và nhỏ nhất.

Lời giải chi tiết:

Hàm số \(y = x\sqrt {1 - {x^2}} \)xác định khi

Hàm số \(y = x\sqrt {1 - {x^2}} \)có đạo hàm là \(y' = \sqrt {1 - {x^2}}  + x.\frac{{ - 2x}}{{2\sqrt {1 - {x^2}} }} = \sqrt {1 - {x^2}}  - \frac{{{x^2}}}{{\sqrt {1 - {x^2}} }}\)

Ta có \(y' = 0 \Leftrightarrow \sqrt {1 - {x^2}}  - \frac{{{x^2}}}{{\sqrt {1 - {x^2}} }} = 0 \Leftrightarrow x =  \pm \frac{{\sqrt 2 }}{2}\).

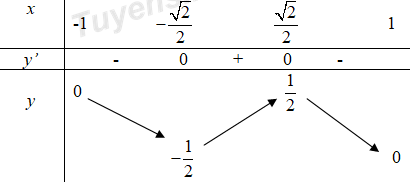
Ta có bảng biến thiên:

Dựa vào bảng biến thiên ta thấy giá trị lớn nhất, nhỏ nhất của hàm số là \(M = \frac{1}{2};\,\,m =  - \frac{1}{2}.\)

\( \Rightarrow M + m = 0.\)

Chọn A.