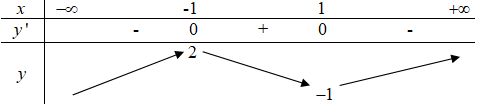Câu hỏi
Tìm tất cả các giá trị tham số \(m\) để đồ thị hàm số \(y = {x^3} - 3x + 1\) luôn cắt đường thẳng \(y = m\) tại ba điểm phân biệt.
- A \( - 1 \le m \le 1.\)
- B \( - 1 < m < 3.\)
- C
\( - 1 < m \le 1.\)
- D \( - 1 < m \le 3.\)
Phương pháp giải:
Vẽ bảng biến thiên của hàm số \(y = {x^3} - 3x + 1\).
Từ đó dựa vào bảng biến thiên để kết luận giá trị của \(m\).
Lời giải chi tiết:
Ta có: \(y' = 3{x^2} - 3 = 0 \Leftrightarrow x = \pm 1\)
Bảng biến thiên:
Dựa vào bảng biến thiê ta thấy để đồ thị hàm số \(y = {x^3} - 3x + 1\) cắt đồ thị hàm số \(y = m\) tại 3 điểm phân biệt thì \( - 1 < m < 2.\)
Chọn C.
Câu hỏi trước
