Câu hỏi
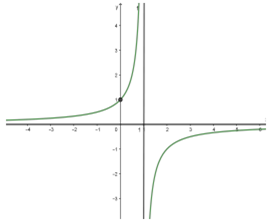
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Biết rằng \(f\left( x \right) = \frac{{ax + b}}{{cx + d}}\); \(g\left( x \right) = f\left( {f\left( x \right)} \right)\). Tìm giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ { - 3; - 1} \right].\)
- A \(-2\)
- B \(2\)
- C \(1\)
- D \( - \frac{4}{3}.\)
Phương pháp giải:
Dựa vào đồ thị để tìm hàm số \(f\left( x \right)\).
Tìm đạo hàm của \(g\left( x \right)\).
Tìm giá trị lớn nhất của \(g\left( x \right)\) rồi kết luận.
Lời giải chi tiết:
Đồ thị hàm số \(f\left( x \right) = \frac{{ax + b}}{{cx + d}}\) nhận đường thẳng \(x = 1\) làm tiệm cận đứng và đường thẳng \(y = 0\) làm tiệm cận ngang; đồng thời đi qua điểm có tọa độ \(\left( {0;1} \right)\)
Do đó \(\left\{ \begin{array}{l} - \frac{d}{c} = 1\\\frac{a}{c} = 0\\\frac{b}{d} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = - c\\d = - c\end{array} \right. \Rightarrow f\left( x \right) = \frac{{0.x - c}}{{cx - c}} = \frac{{ - 1}}{{x - 1}}\)
Ta có \(f\left( x \right) = \frac{{ - 1}}{{x - 1}} \Rightarrow f'\left( x \right) = \frac{1}{{{{\left( {x - 1} \right)}^2}}} > 0\)
Mặt khác \(g\left( x \right) = f\left( {f\left( x \right)} \right) \Rightarrow g'\left( x \right) = f'\left( x \right).f'\left( {f\left( x \right)} \right)\)
Mà \(f'\left( u \right) > 0\)
Suy ra \(g'\left( x \right) > 0\) hay hàm số \(g\left( x \right)\) luôn đồng biến trên \(\mathbb{R}\).
Nên giá trị lớn nhất của \(g\left( x \right)\) trên \(\left[ { - 3; - 1} \right]\) là \(g\left( { - 1} \right) = f\left( {f\left( { - 1} \right)} \right) = f\left( {\frac{1}{2}} \right) = 2\).
Chọn B.