Phương pháp giải:

Gọi chiều rộng của đáy hố ga là x.

Tính chiều cao, chiều dài, diện tích xung quanh, diện tích đáy hố ga theo x.

Lập hàm số biểu diễn tổng diện tích bề mặt hố ga cần xây.

Lập bảng biến thiên, tìm GTNN của hàm số trên. Từ đó suy ra x và tính diện tích đáy hố ga.

Lời giải chi tiết:

Gọi chiều rộng của đáy là x (cm; x > 0).

Khi đó chiều cao của hố ga là 2x và chiều dài của hố ga là \(\frac{{25600}}{{x.2x}} = \frac{{12800}}{{{x^2}}}\) (cm).

Diện tích xung quanh hố ga là:

\({S_{xq}} = 2\left( {x.2x} \right) + 2\left( {\frac{{12800}}{{{x^2}}}.2x} \right) = 4{x^2} + \frac{{51200}}{x}\) \(\left( {c{m^2}} \right)\).

Diện đáy của hố ga là \({S_d} = \frac{{12800}}{{{x^2}}}.x = \frac{{12800}}{x}\) \(\left( {c{m^2}} \right)\).

Tổng diện tích xây hố ga là \(S(x) = 4{x^2} + \frac{{51200}}{x} + \frac{{12800}}{x} = 4{x^2} + \frac{{64000}}{x}\).

\(S'(x) = 8x - \frac{{64000}}{{{x^2}}} = 0 \Leftrightarrow {x^3} = 8000 \Leftrightarrow x = 20\).

Bảng biến thiên:

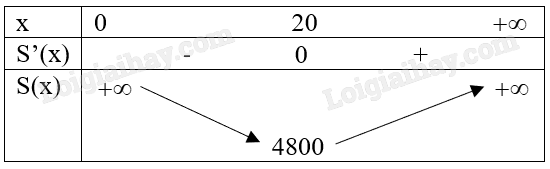
Để xây tiết kiệm nguyên vật liệu nhất thì S(x) phải nhỏ nhất. Khi đó x = 20.

Diện tích đáy hố ga là \({S_d} = \frac{{12800}}{{20}} = 640\) \(\left( {c{m^2}} \right)\).