Phương pháp giải:

Sử dụng tỉ số để tính độ dài cạnh đáy và chiêu cao của hình chóp.

Lời giải chi tiết:

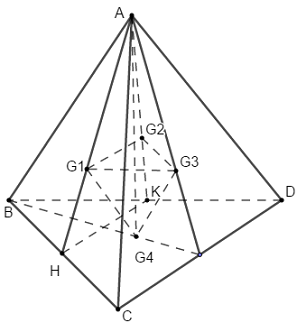
Gọi H,K lần lượt là trung điểm của BC,BD.

\( \Rightarrow {G_1}{G_2} = \dfrac{2}{3}HK = \dfrac{2}{3}.\dfrac{1}{2}.CD = \dfrac{1}{3}CD = a\)

Do đó tam giác \({G_1}{G_2}{G_2}\) là tam giác đều cạnh a\( \Rightarrow {S_{{G_1}{G_2}{G_2}}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

Tứ diện đều ABCD có \({G_4}\) là trọng tâm tam giác đều BDC.

\( \Rightarrow A{G_4} \bot \left( {BCD} \right)\)

Tam giác \(A{G_4}B\) vuông tại \({G_4}\) có:

\(\begin{array}{l}AB = 3a;\,\,\,B{G_4} = \dfrac{{\sqrt 3 }}{3}.3a = a\sqrt 3 \\ \Rightarrow A{G_4} = \sqrt {A{B^2} - BG_4^2}  = a\sqrt 6 \end{array}\)

Mặt khác \(d\left( {{G_4};\left( {{G_1}{G_2}{G_2}} \right)} \right) = \dfrac{1}{3}d\left( {A;\left( {BCD} \right)} \right) = \dfrac{1}{3}.A{G_4} = \dfrac{{a\sqrt 6 }}{3}\) vì \({G_4}\) là trọng tâm tam giác đều BDC.

Khi đó \({V_{{G_1}{G_2}{G_2}{G_4}}} = \dfrac{1}{3}.h.{S_{{G_1}{G_2}{G_2}}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{3}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 2 }}{{12}}\)

Chọn A.