Câu hỏi
Chọn đáp án đúng nhất:
Câu 1:
Thực hiện phép tính :
\(a)\,\,\sqrt {20} - 3\sqrt {125} + 5\sqrt {45} \) \(b)\,\,\frac{3}{{\sqrt 3 - \sqrt 2 }} - 2\sqrt {{{\left( {\sqrt 2 - \sqrt 3 } \right)}^2}} - 5\sqrt 2 \)
- A \(\begin{array}{l}a)\,\,\sqrt 5 \\b)\,\,\sqrt 3 \end{array}\)
- B \(\begin{array}{l}a)\,\,2\sqrt 5 \\b)\,\,\sqrt 3 \end{array}\)
- C \(\begin{array}{l}a)\,\,\sqrt 5 \\b)\,\,2\sqrt 3 \end{array}\)
- D \(\begin{array}{l}a)\,\,2\sqrt 5 \\b)\,\,2\sqrt 3 \end{array}\)
Phương pháp giải:
a) Sử dụng công thức đưa thừa số ra ngoài dấu căn : Với \(B \ge 0\) ta có : \(\sqrt {{A^2}B} = \left| A \right|B = \left\{ \begin{array}{l}AB\,\,\,\,khi\,\,\,\,A \ge 0\\ - AB\,\,\,khi\,\,\,\,A < 0\end{array} \right..\)
b) Sử dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\) và trục căn thức ở mẫu : \(\frac{m}{{\sqrt A - \sqrt B }} = \frac{{m\left( {\sqrt A + \sqrt B } \right)}}{{A - B}}\,\,\,\left( {A,B \ge 0;A \ne B} \right)\)
Lời giải chi tiết:
\(\begin{array}{l}a)\,\,\sqrt {20} - 3\sqrt {125} + 5\sqrt {45} \\ = 2\sqrt 5 - 15\sqrt 5 + 15\sqrt 5 \\ = 2\sqrt 5 \end{array}\)
\(\begin{array}{l}b)\,\,\frac{3}{{\sqrt 3 - \sqrt 2 }} - 2\sqrt {{{\left( {\sqrt 2 - \sqrt 3 } \right)}^2}} - 5\sqrt 2 \\ = \frac{{3\left( {\sqrt 3 + \sqrt 2 } \right)}}{{3 - 2}} - 2\left| {\sqrt 2 - \sqrt 3 } \right| - 5\sqrt 2 \\ = 3\sqrt 3 + 3\sqrt 2 - 2\left( {\sqrt 3 - \sqrt 2 } \right) - 5\sqrt 2 \\ = 3\sqrt 3 + 3\sqrt 2 - 2\sqrt 3 + 2\sqrt 2 - 5\sqrt 2 \\ = \sqrt 3 \end{array}\)
Chọn B.
Câu 2:
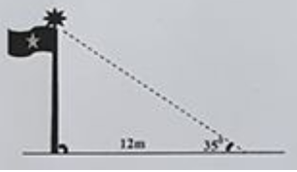
Một cột cờ vuông góc với mặt đất có bóng dài \(12m\), tia nắng của mặt trời tạo với mặt đất một góc là \(35\) (hình vẽ bên). Tính chiều cao của cột cờ.
- A \(6,708m\)
- B \(7,216m\)
- C \(8,402m\)
- D \(9,138m\)
Phương pháp giải:
Sử dụng quan hệ giữa cạnh và góc trong tam giác.
Trong tam giác vuông, cạnh góc vuông này bằng cạnh góc vuông còn lại nhân tan góc đối.
Lời giải chi tiết:
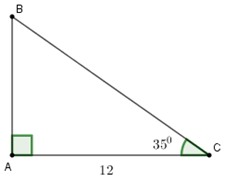
Ta đưa về bài toán: Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 12m,\,\,\,\angle BCA = {35^0}.\) Tính \(AB.\)
Chiều cao cột là \(AB\).
Do \(\Delta ABC\) vuông tại \(A\) nên ta có :
\(\begin{array}{l}AB = AC.\tan C\\\,\,\,\,\,\,\,\,\, = 12.\tan 35^\circ \\\,\,\,\,\,\,\,\,\, = 8,402\,\,\left( m \right)\end{array}\)
Chọn C.