Phương pháp giải:

a) Với \(a > 0\) thì hàm số \(y = a{x^2} + bx + c\) đồng biến trên \(\left( { - \frac{b}{{2a}}; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\)

b) Lập BBT của hàm số đã cho trên đoạn \(\left[ { - 3;2} \right]\) từ đó xác định GTLN và GTNN.

Lời giải chi tiết:

a) Lập bảng biến thiên và vẽ đồ thị của hàm số \(y = {x^2} - 2x + 2\).

Tập xác định: \(D = R\)

Đỉnh Parbol: \(I\left( {1;1} \right)\)

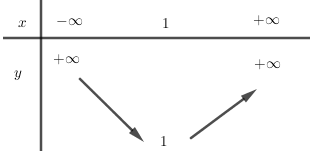
BBT:

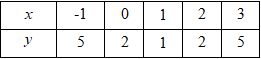
Bảng giá trị:

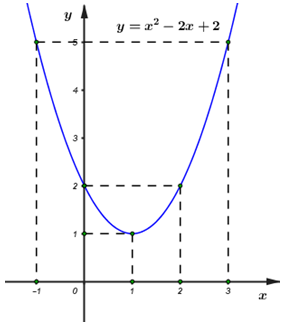
Đồ thị hàm số:

b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^2} - 2x + 2\) trên đoạn \(\left[ { - 3;2} \right]\).

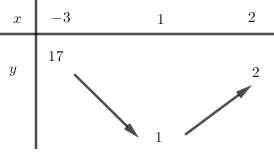
BBT của hàm số \(y = {x^2} - 2x + 2\) trên đoạn \(\left[ { - 3;2} \right]\)

Từ BBT ta có:  GTLN của hàm số trên \(\left[ { - 3;2} \right]\) là \(y = 17 \Leftrightarrow x =  - 3\)

GTNN của hàm số trên \(\left[ { - 3;2} \right]\) là \(y = 2 \Leftrightarrow x = 2\)

Chọn D.