Phương pháp giải:

1) Tìm hoành độ đỉnh, trục đối xứng của Parabol, từ đó suy ra khoảng đồng biến nghịch biến và lập bảng biến thiên.

2) Xét phương trình hoành độ giao điểm tìm nghiệm.

3) Nhận xét điều kiện từ đồ thị đã vẽ.

Lời giải chi tiết:

1) Lập bảng biến thiên và vẽ đồ thị \(\left( P \right)\) của hàm số \(y = {x^2} + 2x-3\)

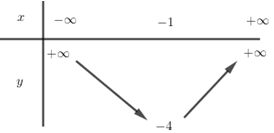
Ta có: \( - \frac{b}{{2a}} =  - \frac{2}{{2.1}} =  - 1, - \frac{\Delta }{{4a}} =  - 4\)

Vì \(a = 1 > 0\) nên hàm số nghịch biến trên \(\left( { - \infty ; - 1} \right)\) và đồng biến trên \(\left( { - 1; + \infty } \right)\).

Bảng biến thiên:                        

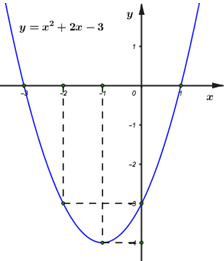
Đồ thị có: Đỉnh \(P\left( { - 1; - 4} \right)\), cắt \(Ox\) tại \(\left( {1;0} \right),\left( { - 3;0} \right)\), cắt \(Oy\) tại \(\left( {0; - 3} \right)\), đi qua điểm \(\left( { - 2; - 3} \right)\).

Trục đối xứng \(x =  - 1\), bề lõm hướng lên trên.

2) Tìm tọa độ giao điểm của \(\left( P \right)\)và đường thẳng \(d:{\rm{ }}y{\rm{ }} = {\rm{ }}x{\rm{ }}--{\rm{ }}1\)

Xét phương trình hoành độ giao điểm của hai đồ thị hàm số:

\({x^2} + 2x - 3 = x - 1\) \( \Leftrightarrow {x^2} + x - 2 = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}x = 1,y = 0\\x =  - 2,y =  - 3\end{array} \right.\)

Vậy giao điểm là \(A\left( {1;0} \right),B\left( { - 2; - 3} \right)\).

3) Tìm \(m\) sao cho đường thẳng \(y{\rm{ }} = {\rm{ }}2m\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ âm.

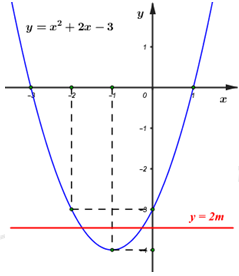
Đường thẳng \(y = 2m\) đi qua điểm \(\left( {0;2m} \right)\) và song song hoặc trùng với trục hoành.

Từ đồ thị ta thấy YCBT thỏa mãn khi \( - 4 < 2m <  - 3 \Leftrightarrow  - 2 < m <  - \frac{3}{2}\).

Vậy \( - 2 < m <  - \frac{3}{2}\).

Chọn A.