Phương pháp giải:

a) Tìm trục đối xứng, đỉnh, khoảng đồng biến nghịch biến, lập bảng biến thiên.

Tìm tọa độ các điểm đi qua và vẽ đồ thị.

b) Tìm điều kiện để phương trình có hai nghiệm phân biệt.

- Tìm hai nghiệm và suy ra tọa độ, dùng điều kiện \(OA = 3OB\) tìm \(m\).

Lời giải chi tiết:

a) Lập bảng biến thiên và vẽ đồ thị hàm số trên với \(m = 3.\)

Với \(m = 3\) ta có hàm số \(y = {x^2} - 4x + 3\)

Trục đối xứng \(x = 2.\)

Đỉnh parabol \(I\left( {2; - 1} \right)\)

Vì \(a > 0\) nên đồ thị hàm số quay bề lõm lên trên

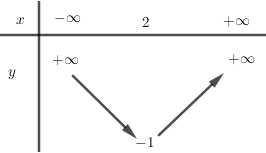
BBT:

Hàm số đồng biến trên \(\left( {2; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ;2} \right)\)

Bảng giá trị:

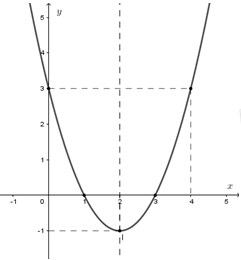
Đồ thị hàm số:

b) Tìm  \(m\) sao cho đồ thị cắt \(Ox\) tại \(2\) điểm phân biệt  \(A,\,B\) với  \(OA = 3OB.\)  (1,5đ)

Xét phương trình hoành độ giao điểm \({x^2} - 4x + m = 0\) (1)

Đồ thị cắt \(Ox\) tại hai điểm phân biệt \( \Leftrightarrow \Delta ' = 4 - m > 0 \Leftrightarrow m < 4\).

Khi đó (1) có hai nghiệm phân biệt \({x_1} = 2 - \sqrt {4 - m} ,{x_2} = 2 + \sqrt {4 - m} \).

TH1: \(A\left( {2 + \sqrt {4 - m} ;0} \right),B\left( {2 - \sqrt {4 - m} ;0} \right)\).

\(OA = 3OB\) \( \Leftrightarrow 2 + \sqrt {4 - m}  = 3\left| {2 - \sqrt {4 - m} } \right|\)

\( \Leftrightarrow 4 + 4 - m + 4\sqrt {4 - m} \) \( = 9\left( {4 + 4 - m - 4\sqrt {4 - m} } \right)\)

\( \Leftrightarrow 5\sqrt {4 - m}  = 8 - m\) \( \Leftrightarrow \left\{ \begin{array}{l}8 - m \ge 0\\25\left( {4 - m} \right) = 64 - 16m + {m^2}\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}m \le 8\\{m^2} + 9m - 36 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m \le 8\\m = 3,m =  - 12\end{array} \right. \Leftrightarrow m = 3\,\,\,\left( {tm} \right)\)

Vậy \(m = 3\).

TH2: \(A\left( {2 - \sqrt {4 - m} ;0} \right),B\left( {2 + \sqrt {4 - m} ;0} \right)\).

\(OA = 3OB\) \( \Leftrightarrow \left| {2 - \sqrt {4 - m} } \right| = 3\left( {2 + \sqrt {4 - m} } \right)\)

\( \Leftrightarrow 4 + 4 - m - 4\sqrt {4 - m} \) \( = 9\left( {4 + 4 - m + 4\sqrt {4 - m} } \right)\)

\( \Leftrightarrow 5\sqrt {4 - m}  = m - 8\) (vô nghiệm do \(m < 4\) thì \(m - 8 < 0\))

Vậy có một giá trị duy nhất là \(m = 3\).

Chọn C.