Câu hỏi
Trong không gian cho hình vuông \(ABCD\) cạnh \(a\). Gọi \(I\) và \(H\) lần lượt là trung điểm của các cạnh \(AB\) và \(CD\). Khi quay hình vuông \(ABCD\), kể cả các điểm trong nó, xung quanh đường thẳng \(IH\) ta được một khối trụ tròn xoay có thể tích là
- A \(V = \pi {a^3}\)
- B \(V = \dfrac{{\pi {a^3}}}{2}\)
- C \(V = \dfrac{{\pi {a^3}}}{4}\)
- D \(V = \dfrac{{\pi {a^3}}}{3}\)
Phương pháp giải:
- Khi quay hình vuông và các điểm bên trong nó xung qunh một đường thẳng đi qua trung điểm 2 cạnh đối diện ta được một hình trụ có chiều cao và đường kính đáy bằng cạnh hình vuông.
- Thể tích của khối trụ có bán kính đáy bằng \(r\) và chiều cao bằng \(h\) là \(V = \pi {r^2}h\).
Lời giải chi tiết:
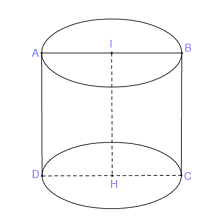
\(I\) và \(H\) là trung điểm của 2 cạnh đối \(AB\) và \(CD\) nên khi quay hình vuông \(ABCD\) và các điểm bên trong nó quanh đường thẳng \(IH\) ta được một khối trụ có chiều cao là \(IH\) và hai đáy có đường kính là \(AB\) và \(CD\).
Do vậy khối trụ trên có chiều cao là \(h = IH = a\) và bán kính đáy là \(r = IA = \dfrac{{AB}}{2} = \dfrac{a}{2}\).
Thể tích của khối trụ tròn xoay tạo thành là :
\(V = \pi .IH.I{A^2} = \pi .a.{\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{\pi {a^3}}}{4}\)
Chọn C.







