Câu hỏi
Cắt một hình trụ bằng một mặt phẳng đi qua trục của nó, ta được thiết diện là một hình vuông cạnh \(2a.\) Diện tích xung quanh của hình trụ bằng :
- A \(16\pi {a^2}.\)
- B \(2\pi {a^2}.\)
- C \(8\pi {a^2}.\)
- D \(4\pi {a^2}.\)
Phương pháp giải:
Diện tích xung quanh của hình trụ có bán kính đáy \(r\) và đường sinh \(l\) là \({S_{xq}} = 2\pi rl\)
Lời giải chi tiết:
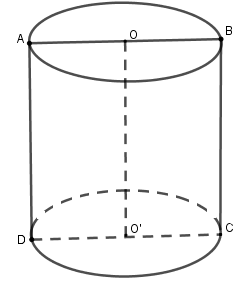
Thiết diện qua trục là hình vuông \(ABCD\) như hình vẽ
Bán kính đáy \(R = \dfrac{{DC}}{2} = \dfrac{{2a}}{2} = a\)
Đường sinh: \(l = BC = 2a\)
Diện tích xung quanh hình trụ: \({S_{xq}} = 2\pi rl = 2\pi .a.2a = 4\pi {a^2}\)
Chọn D.
Câu hỏi trước
