Câu hỏi
Một con lắc lò xo được treo thẳng đứng gồm lò xo có độ cứng k và vật nặng khối lượng 2m. Từ vị trí cân bằng, đưa vật tới vị trí lò xo không bị biến dạng rồi thả nhẹ cho vật dao động. Khi vật xuống dưới vị trí thấp nhất thì khối lượng của vật đột ngột giảm xuống còn một nửa. Bỏ qua mọi ma sát và gia tốc trọng trường là g. Biên độ dao động của vật sau khi khối lượng giảm là
- A \(\dfrac{{2mg}}{k}\)
- B \(\dfrac{{mg}}{k}\)
- C \(\dfrac{{3mg}}{k}\)
- D \(\dfrac{{3mg}}{{2k}}\)
Phương pháp giải:
Độ biến dạng của lò xo ở vị trí cân bằng: \(\Delta l = \dfrac{{mg}}{k}\)
Độ dịch chuyển vị trí cân bằng: \(\Delta x = \dfrac{{\Delta mg}}{k}\)
Lời giải chi tiết:
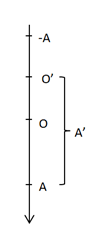
Ban đầu, đưa vật tới vị trí lò xo không biến dạng rồi thả nhẹ vật, biên độ dao động khi đó là:
\(A = \Delta l = \dfrac{{2mg}}{k}\)
Khi khối lượng vật giảm còn một nửa, vị trí cân bằng dịch chuyển lên trên một đoạn:
\({\rm{OO}}' = \Delta x = \dfrac{{\Delta mg}}{k} = \dfrac{{mg}}{k}\)
Biên độ mới của dao động:
\(A' = A + {\rm{OO'}} = \dfrac{{2mg}}{k} + \dfrac{{mg}}{k} = \dfrac{{3mg}}{k}\)
Chọn C.







