Câu hỏi
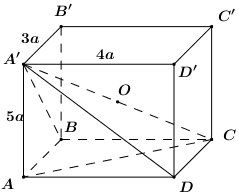
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 3a,\,\,AD = 4a,\,\,AA' = 5a\). Bán kính mặt cầu ngoại tiếp hình chóp \(A'.ABCD\) bằng:
- A \(5a.\)
- B \(\frac{{5a}}{2}.\)
- C \(\frac{{5a\sqrt 2 }}{2}.\)
- D \(5a\sqrt 2 .\)
Phương pháp giải:
Thể tích khối nón chiều cao \(h\), bán kính đáy \(r\) là \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết:
Gọi \(O\) là trung điểm của \(A'C\), khi đó \(O\) là tâm mặt cầu ngoại tiếp khối hộp chữ nhật \(ABCD.A'B'C'D'\).
\( \Rightarrow OA' = OA = OB = OC = OD \Rightarrow O\) cũng là tâm mặt cầu ngoại tiếp chóp \(A'ABCD\).
Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}} = 5a\).
Áp dụng định lí Pytago trong tam giác vuông \(A'AC\) có:
\(A'C = \sqrt {AA{'^2} + A{C^2}} = \sqrt {{{\left( {5a} \right)}^2} + {{\left( {5a} \right)}^2}} = 5a\sqrt 2 \).
Vậy bán kính mặt cầu ngoại tiếp chóp \(A'.ABCD\) là \(R = \frac{1}{2}A'C = \frac{{5a\sqrt 2 }}{2}\).
Chọn C.