Câu hỏi
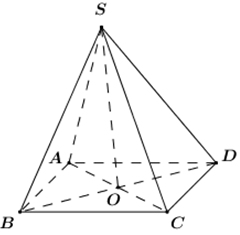
Cho hình chóp đều \(S.ABCD\) có \(ABCD\) là hình vuông cạnh \(2a\) và \(SA \bot SC.\) Bán kính mặt cầu ngoại tiếp hình chóp đều đã cho bằng:
- A \(\frac{a}{{\sqrt 2 }}.\)
- B \(a\sqrt 2 .\)
- C \(a.\)
- D \(2a.\)
Phương pháp giải:
Tâm mặt cầu ngoại tiếp hình chóp là điểm cách đều tất cả các đỉnh của hình chóp.
Lời giải chi tiết:
Gọi \(O = AC \cap BD \Rightarrow OA = OB = OC = OC\).
Xét tam giác vuông \(SAC\) có trung tuyến \(SO \Rightarrow OS = \frac{1}{2}AC = OA = OC\).
\( \Rightarrow OA = OB = OC = OD = OS\).
\( \Rightarrow O\) là tâm mặt cầu ngoại tiếp khối chóp \(S.ABC\) và bán kính khối cầu là \(R = OA\).
Vì \(ABCD\) là hình vuông cạnh \(2a\) nên \(AC = 2a\sqrt 2 \Rightarrow OA = a\sqrt 2 \).
Vậy \(R = a\sqrt 2 \).
Chọn B.