Phương pháp giải:

Tìm tâm mặt cầu ngoại tiếp hình chóp \(S.ABC\) bằng cách:

- Gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).

- Qua \(O\) dựng đường thẳng \(d\) vuông góc với mặt phẳng \(\left( {ABC} \right)\).

- Dựng mặt phẳng \(\left( \alpha  \right)\) là mặt phẳng trung trực của một cạnh bên bất kì cắt đường thẳng  \(d\) tại \(I\) thì \(I\) chính là tâm mặt cầu ngoại tiếp khối chóp.

Suy ra bán kính của hình chóp \(R = IS = IA = IB = IC\).

Lời giải chi tiết:

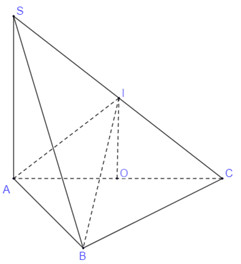
Gọi \(O\) là trung điểm \(AC\) và \(I\) là trung điểm \(SC\).

Do tam giác \(ABC\) vuông tại \(B\) nên \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).

\(IO\) là đường trung bình trong tam giác \(SAC\) nên \(IO\parallel SA\) mà \(SA \bot \left( {ABC} \right) \Rightarrow OI \bot \left( {ABC} \right)\).

\(IO\) đi qua tâm đường tròn ngoại tiếp tam giác \(ABC\) và vuông góc với mp\(\left( {ABC} \right)\) nên \(IA = IB = IC\)     (1)

Mặt khác tam giác \(SAC\) vuông tại \(A,\) có trung tuyến \(AI\) nên \(AI = \dfrac{1}{2}SC = SI = IC\)                        (2)

Từ (1) và (2) suy ra \(IA = IB = IC = IS\) do đó \(I\) là tâm mặt cầu ngoại tiếp khối chóp \(S.ABC\)

Áp dụng định lí Pytago ta có: \(AC = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{6^2} + {8^2}}  = 10\)

                                               \(SC = \sqrt {S{A^2} + A{C^2}}  = \sqrt {{{10}^2} + {{10}^2}}  = 10\sqrt 2 \) 

Suy ra \(R = IA = \dfrac{1}{2}SC = \dfrac{1}{2}.10\sqrt 2  = 5\sqrt 2 \).

Vậy bán kính mặt cầu ngoại tiếp hình chóp bằng \(5\sqrt 2 \).

Chọn C.