Câu hỏi
Cho hình lập phương \(ABCD.A'B'C'D'\) có \(AC' = a\sqrt 3 \). Tính bán kính \(R\) của mặt cầu tiếp xúc với 6 mặt của hình lập phương trên
- A \(R = 2a\)
- B \(R = \dfrac{{a\sqrt 3 }}{2}\)
- C \(R = a\sqrt 3 \)
- D \(R = \dfrac{a}{2}\)
Phương pháp giải:
Mặt cầu tiếp xúc với 6 mặt của hình lập phương có đường kính lớn bằng cạnh của hình lập phương.
Lời giải chi tiết:
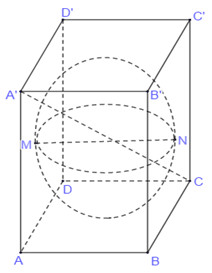
\(ABCD.A'B'C'D'\) là hình lập phương nên ta có:
\(\begin{array}{l}AC' = a\sqrt 3 \Leftrightarrow AC{'^2} = 3{a^2} \Leftrightarrow A{C^2} + CC{'^2} = 3{a^2}\\ \Leftrightarrow A{B^2} + B{C^2} + CC{'^2} = 3{a^2} \Leftrightarrow 3A{B^2} = 3{a^2} \Rightarrow AB = a\end{array}\)
Mặt cầu tiếp xúc với 6 mặt của hình lập phương có đường kính lớn bằng cạnh của hình lập phương nên: \(2R = AB \Rightarrow R = \dfrac{a}{2}\).
Vậy bán kính của mặt cầu tiếp xúc với 6 mặt của hình lập phương là \(R = \dfrac{a}{2}\).
Chọn D.







